Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}\widehat{DCA}=\widehat{HCA}\\\widehat{DCA}+\widehat{DAC}=90^0\\\widehat{HCA}+\widehat{HBA}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{HBA}=\widehat{DAC}\)
\(\left\{{}\begin{matrix}\widehat{DAC}+\widehat{BAE}=90^0\\\widehat{HBA}+\widehat{HAB}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{BAE}=\widehat{HAB}\)
Có \(\left\{{}\begin{matrix}AH=AE=R\\\widehat{BAE}=\widehat{HAB}\\\text{AB chung}\end{matrix}\right.\) \(\Rightarrow\Delta AHB=\Delta AEB\)
\(\Rightarrow\widehat{E}=\widehat{H}=90^0\Rightarrow BE\) là tiếp tuyến

1) Ta có: \(BC^2=5^2=25\)
\(AB^2+AC^2=3^2+4^2=25\)
Do đó: \(BC^2=AB^2+AC^2\)(=25)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\)
2)
a) Xét (A) có
H∈(A)
BH⊥AH tại H(gt)
Do đó: BH là tiếp tuyến của (A)(Dấu hiệu nhận biết tiếp tuyến của đường tròn)
Xét (A) có
H∈(A)
CH⊥AH tại H(gt)
Do đó: CH là tiếp tuyến của (A)(Dấu hiệu nhận biết tiếp tuyến đường tròn)
Xét (A) có
CH là tiếp tuyến có H là tiếp điểm(cmt)
CE là tiếp tuyến có E là tiếp điểm(gt)
Do đó: AC là tia phân giác của \(\widehat{EAH}\)(Tính chất hai tiếp tuyến cắt nhau)
⇒\(\widehat{EAH}=2\cdot\widehat{HAC}\)
Xét (A) có
BH là tiếp tuyến có H là tiếp điểm(gt)
BD là tiếp tuyến có D là tiếp điểm(gt)
Do đó: AB là tia phân giác của \(\widehat{HAD}\)(Tính chất hai tiếp tuyến cắt nhau)
⇒\(\widehat{HAD}=2\cdot\widehat{BAH}\)
Ta có: \(\widehat{EAH}+\widehat{HAD}=\widehat{EAD}\)(Tia AH nằm giữa hai tia AE,AD)
\(\Leftrightarrow2\cdot\widehat{BAH}+2\cdot\widehat{CAH}=\widehat{EAD}\)
\(\Leftrightarrow\widehat{EAD}=2\cdot\left(\widehat{BAH}+\widehat{CAH}\right)\)
\(\Leftrightarrow\widehat{EAD}=2\cdot90^0=180^0\)
hay E,A,D thẳng hàng(đpcm)

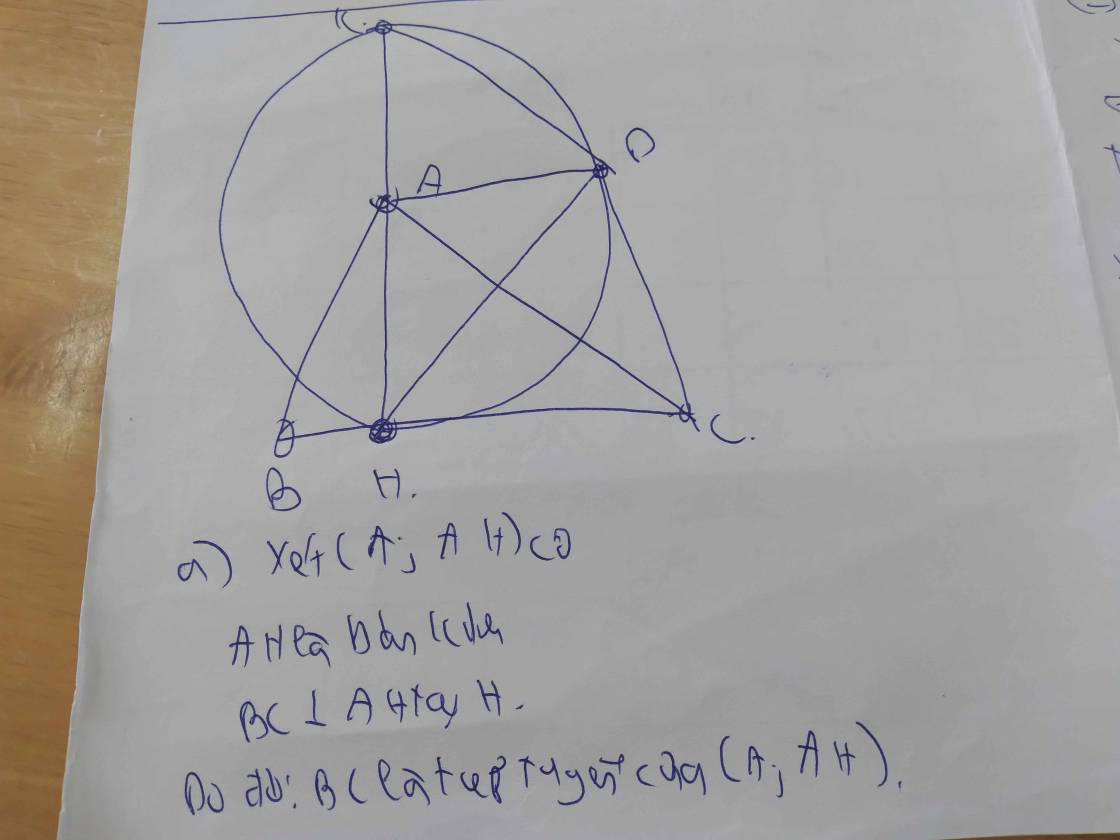
a: Xét (A;AH) có
AH là bán kính
BC\(\perp\)AH tại H
Do đó: BC là tiếp tuyến của (A;AH)
b: ΔAHI cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAI
Xét ΔAHB và ΔAIB có
AH=AI
\(\widehat{HAB}=\widehat{IAB}\)
AB chung
Do đó: ΔAHB=ΔAIB
=>\(\widehat{AHB}=\widehat{AIB}=90^0\)
=>BI là tiếp tuyến của (A;AH)
c:
\(\widehat{HAB}+\widehat{HAC}=\widehat{BAC}=90^0\)
=>\(\widehat{HAC}=90^0-\widehat{HAB}\)
\(\widehat{KAH}+\widehat{HAI}=180^0\)(hai góc kề bù)
=>\(\widehat{KAH}+2\cdot\widehat{BAH}=180^0\)
=>\(\widehat{KAH}=180^0-2\cdot\widehat{BAH}=2\left(90^0-\widehat{BAH}\right)=2\cdot\widehat{CAH}\)
=>AC là phân giác của góc KAH
Xét ΔAHC và ΔAKC có
AH=AK
\(\widehat{HAC}=\widehat{KAC}\)
AC chung
Do đó: ΔAHC=ΔAKC
=>CH=CK
CH+HB=CB
mà CH=CK và BH=BI
nên CK+BI=BC