Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn tự vẽ hình nka !!!
a) , b) Theo định lí Py - ta - go trong \(\Delta ABC\)vuông tại A , ta có :
\(BC^2=AB^2+AC^2=15^2+20^2=625\)\(\Leftrightarrow BC=\sqrt{625}=25\left(cm\right)\)
Xét \(\Delta AHB\)và \(\Delta CAB\)có :
\(\widehat{ABC}\)chung ; \(\widehat{BHA}=\widehat{BAC}=90\)độ
\(\Leftrightarrow\Delta AHB\infty\Delta CAB\left(g.g\right)\)
Ta có tỉ lệ : \(\frac{AH}{AC}=\frac{BH}{AB}=\frac{AB}{BC}\)
\(\Leftrightarrow AH=\frac{AB\cdot AC}{BC}=\frac{15\cdot20}{25}=12\left(cm\right)\)
\(\Leftrightarrow BH=\frac{AB^2}{BC}=\frac{15^2}{25}=9\left(cm\right)\)
\(\Leftrightarrow CH=BC-BH=25-9=16\left(cm\right)\)
c) ta có : \(AM=\frac{BC}{2}=\frac{25}{2}=12,5\left(cm\right)\) ( do AM là đường trung tuyến ứng với cạnh huyền BC )
Theo định lí Py - ta - go trong \(\Delta AHM\)vuông tại H , ta có :
\(HM^2=AM^2-AH^2=12,5^2-12^2=12,25\)\(\Leftrightarrow HM=\sqrt{12,25}=3,5\left(cm\right)\)
\(\Rightarrow S_{AHM}=\frac{1}{2}\cdot AH\cdot HM=\frac{3,5\cdot12}{2}=\frac{42}{2}=21\left(cm^2\right)\)
TK CKO MK NKA !!!

\(\Delta ABC\)có : AB2 + AC2 = (4,5)2 + 62 = 56,25 = (7,5)2 = BC2 nên\(\Delta ABC\)vuông tại A
=> Trung tuyến AM bằng nửa cạnh huyền BC và bằng : 7,5 : 2 = 3,75 (cm)

Xét 2 tam giác ABC và HBA, ta có
A= H= 900
B chung
=> tam giác ABCđồng dạng với tam giác HBA
b) Áp dụng định lí pi ta go, ta có
BC2 = AB2+AC2
BC2= 212 +282=1225
=> BC=35
... CM tương tự để ra AM và AH

Xét \(\Delta ABC\&\Delta ABH\) ta có:
\(\widehat{A}=\widehat{B}=90^o\left(gt\right)\\ \widehat{B}=\widehat{B}\\\Rightarrow \Delta ABC\&\sim ABH\)
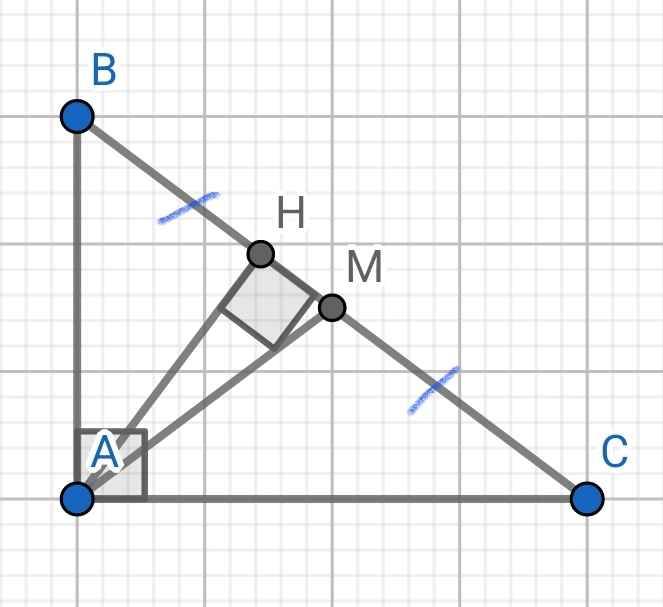
Xét ∆AHB và ∆CBA có:
∠AHB = ∠CAB = 90⁰
∠B chung
⇒ ∆AHB ∽ ∆CBA (g-g)