Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả thiết tương đương:
\(a^4+b^4+c^4+2b^2c^2=2a^2\left(b^2+c^2\right)+2b^2c^2\)
\(\Leftrightarrow a^4+\left(b^2+c^2\right)^2=2a^2\left(b^2+c^2\right)+2b^2c^2\)
\(\Leftrightarrow\left(b^2+c^2-a^2\right)^2=2b^2c^2\)
\(\Leftrightarrow b^2+c^2-a^2=\pm\sqrt{2}bc\)
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{\pm\sqrt{2}bc}{2bc}=\pm\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}A=45^0\\A=135^0\end{matrix}\right.\)

Gọi G là giao điểm của AM và BN.
Theo công thức tính độ dài đường trung tuyến: \(AM^2=\dfrac{2b^2+2c^2-a^2}{4}\);
\(BN^2=\dfrac{2c^2+2a^2-b^2}{4}\).
Từ đó \(AG^2=\dfrac{4}{9}AM^2=\dfrac{2b^2+2c^2-a^2}{9}\); \(BG^2=\dfrac{4}{9}BN^2=\dfrac{2c^2+2a^2-b^2}{9}\).
Do đó \(AG^2+BG^2=\dfrac{a^2+b^2+4c^2}{9}=\dfrac{9c^2}{9}=c^2=AB^2\).
Theo định lý Pythagoras đảo thì tam giác AGB vuông tại G.
Vậy góc giữa 2 trung tuyến AM và BN là 90o.

a) Ta thấy \(\overrightarrow{AB}\left(3;2\right)\) và \(\overrightarrow{AC}\left(4;-3\right)\). Vì \(\dfrac{3}{4}\ne\dfrac{2}{-3}\) nên A, B, C không thẳng hàng.
b) Ta có \(\overrightarrow{BC}\left(1;-5\right)\)
Do vậy \(AB=\left|\overrightarrow{AB}\right|=\sqrt{3^2+2^2}=\sqrt{13}\)
\(AC=\left|\overrightarrow{AC}\right|=\sqrt{4^2+\left(-3\right)^2}=5\)
\(BC=\left|\overrightarrow{BC}\right|=\sqrt{1^2+\left(-5\right)^2}=\sqrt{26}\)
\(\Rightarrow C_{ABC}=AB+AC+BC=5+\sqrt{13}+\sqrt{26}\)
c) Gọi M, N, P lần lượt là trung điểm BC, CA, AB.
\(\Rightarrow P=\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2}\right)=\left(-\dfrac{3}{2};3\right)\)
\(N=\left(\dfrac{x_A+x_C}{2};\dfrac{y_A+y_C}{2}\right)=\left(-1;\dfrac{1}{2}\right)\)
\(M=\left(\dfrac{x_B+x_C}{2};\dfrac{y_B+y_C}{2}\right)=\left(\dfrac{1}{2};\dfrac{3}{2}\right)\)
d) Gọi G là trọng tâm tam giác ABC thì \(G=\left(\dfrac{x_A+x_B+x_C}{3};\dfrac{y_A+y_B+y_C}{3}\right)=\left(-\dfrac{2}{3};\dfrac{5}{3}\right)\)
e) Gọi \(D\left(x_D;y_D\right)\) là điểm thỏa mãn ycbt.
Để ABCD là hình bình hành thì \(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\left(3;2\right)=\left(1-x_D;-1-y_D\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}3=1-x_D\\2=-1-y_D\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D=-2\\y_D=-3\end{matrix}\right.\)
\(\Rightarrow D\left(-2;-3\right)\)
f) Bạn xem lại đề nhé.

BC=a; AC=b; AB=c
Từ C dựng đường thẳng vuông góc với AB tại H
\(\frac{a}{bc}+\frac{1}{b}=\frac{1}{c}+\frac{1}{a+b-c}.\)
\(\Rightarrow a\left(a+b-c\right)+c\left(a+b-c\right)=b\left(a+b-c\right)+bc\)
\(\Rightarrow a^2+ab-ac+ac+bc-c^2=ab+b^2-bc+bc\)
\(\Rightarrow a^2-b^2-c^2+bc=0\) (*)
Ta có \(AB=c=AH+BH\Rightarrow c^2=AH^2+BH^2+2.AH.BH\) (**)
Xét tg vuông ACH có
\(AH^2=AC^2-CH^2=b^2-CH^2\)
Xét tg vuông BCH có
\(BH^2=BC^2-CH^2=a^2-CH^2\)
Thay giá trị của \(AH^2\) và \(BH^2\) vào (**) ta có
\(c^2=b^2-CH^2+a^2-CH^2+2.AH.BH=b^2+a^2-2.CH^2+2.AH.BH\) Thay vào (*) ta có
\(a^2-b^2-\left(b^2+a^2-2.CH^2+2.AH.BH\right)+bc=0\)
\(\Rightarrow-2.b^2+2.CH^2-2.AH.BH+bc=0\)
\(\Rightarrow-2\left(b^2-CH^2\right)-2.AH.BH+bc=0\)
\(\Rightarrow-2.AH^2-2.AH.BH+bc=0\)
\(\Rightarrow bc=2.AH\left(AH+BH\right)=2.AH.AB=2.AH.c\Rightarrow b=AC=2.AH\)
Xét tg vuông ACH có
\(\cos A=\frac{AH}{AC}=\frac{AH}{2.AH}=\frac{1}{2}\Rightarrow\widehat{A}=60^o\left(dpcm\right)\)

Chọn B.
Diện tích tam giác ABC là
S = ½. AC. BC.sinC = ½.a.b.sinC
Vì a; b không đổi và sinC ≤ 1 nên suy ra S ≤ ab/2
Dấu xảy ra khi và chỉ khi sinC = 1 hay ![]()
Vậy giá trị lớn nhất của diện tích tam giác ABC là ab/2.

Lời giải:
Áp dụng BĐT Cauchy-Schwarz:
\(T=\frac{\frac{1}{a^2}}{\frac{1}{b}+\frac{1}{c}}+\frac{\frac{1}{b^2}}{\frac{1}{c}+\frac{1}{a}}+\frac{\frac{1}{c^2}}{\frac{1}{a}+\frac{1}{b}}\geq \frac{(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})^2}{2(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})}=\frac{1}{2}(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})\)
\(\geq \frac{1}{2}.3\sqrt[3]{\frac{1}{abc}}=\frac{3}{2}\) (theo BĐT AM-GM)
Vậy $T_{\min}=\frac{3}{2}$.
Giá trị này đạt tại $a=b=c=1$

Chọn D.
Diện tích tam giác ABC ban đầu là
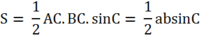
Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là
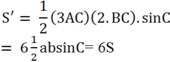

\(\left(a+b+c\right)\left(a+b-c\right)=3ab\)
\(\Leftrightarrow\left(a+b\right)^2-c^2=3ab\)
\(\Leftrightarrow a^2+b^2+2ab-c^2=3ab\)
\(\Leftrightarrow a^2+b^2-c^2=ab\)
\(\Leftrightarrow\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{1}{2}\)
\(\Rightarrow cosC=\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{1}{2}\)
\(\Rightarrow C=60^0\)