K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

3 tháng 5 2021
a,Xét tg DHB và tg DCA có: ^HDB=^CDA=90 độ, ^DBH=^DAC ( cùng phụ với hai góc bằng nhau BHD=^AHE)
Do đó: tg HDB đồng dạng tg DCA (g.g)
Suy ra: HD/DC=BD/DA-> bd*dc=dh*da
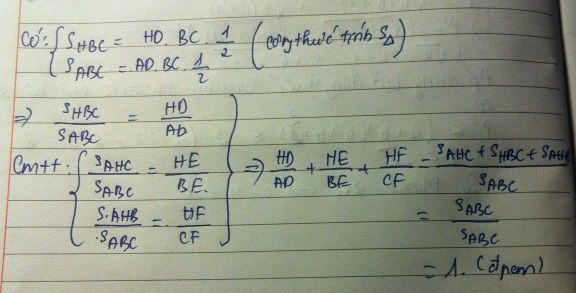
b, HD/HA=SBHC/SABC
HE/BE=SAHC/SABC
HF/CF=SHAB/SABC
HD/HA+HE/BE+HF/CF=SBHC/SABC+SAHC/SABC+SAHB/SABC=1

11 tháng 4 2019
Mấy câu trên bạn lm được rồi mimhf sẽ không giải nữa mà chỉ làm câu d thôi.
Ta có : các điểm D; E; F lần lượt nằm trên các cạnh AC; AB; BC
Mà 3 đoạn thẳng AF; BD; CE đồng quy tại H
Áp dụng định lý Ceeva vào tam giác ABC ta được:
EA/EB . FB/FC . DC/DA = 1
 đó nha bn
đó nha bn
Với \(AF;\) \(BD;\) \(CE\) lần lượt là ba đường cao ứng với các cạnh \(BC;\) \(AC;\) \(AB\) của \(\Delta ABC\), ta có:
\(\frac{S_{BHC}}{S_{ABC}}=\frac{\frac{1}{2}.HF.BC}{\frac{1}{2}.AF.BC}=\frac{HF}{AF}\) \(\left(1\right)\)
\(\frac{S_{AHC}}{S_{ABC}}=\frac{\frac{1}{2}.HD.AC}{\frac{1}{2}.CD.AC}=\frac{HD}{CD}\) \(\left(2\right)\)
\(\frac{S_{AHB}}{S_{ABC}}=\frac{\frac{1}{2}.HE.AB}{\frac{1}{2}.BE.AB}=\frac{HE}{BE}\) \(\left(3\right)\)
Cộng từng vế \(\left(1\right);\) \(\left(2\right)\) và \(\left(3\right)\), với chú ý rằng \(S_{BHC}+S_{AHC}+S_{AHB}=S_{ABC}\), ta được:
\(\frac{HF}{AF}+\frac{HD}{CD}+\frac{HE}{BE}=\frac{S_{BHC}+S_{AHC}+S_{AHB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
Vậy, ....