Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d) A là trung điểm của EF khi 3 điểm E,A,F thẳng hàng và AE=AI
Do đó: \(\widehat{BAC}=90^o\)
Nhận xét: Trường hợp tam giác đã cho có 1 góc tù các đường trung trực của 2 cạnh cắt nhau tại 1 điểm ta cũng có bài toán kết luận tương tự
Nguồn: Hải Ah

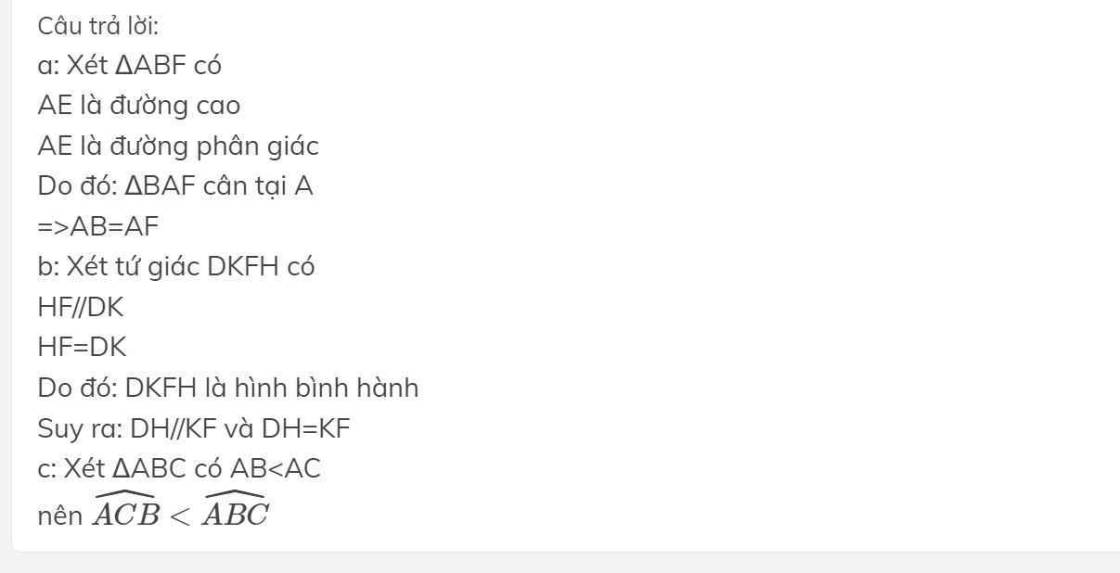
Bài 1 a, xét tam giác ABD và tam giác HBD có:
BD cạnh chung
\(\widehat{ABD}\)=\(\widehat{HBD}\)(gt)
\(\Rightarrow\)tam giác ABD = tam giác HBD( CH-GN)
\(\Rightarrow\)AB=HB
b,trên tia đối của tia DH lấy O sao cho HD=DO
xét tam giác ADO và tam giác CDH có:
DH=DO( theo trên)
\(\widehat{ADO}\)=\(\widehat{CDH}\)( Vì đối đỉnh)
\(\Rightarrow\)tam giác ADO=tam giác CDH( CH-GN)\(\Rightarrow\)AD=CD

a) Ta có AB là trung trực của ME và AC là trung trực của MF. Vì góc A = 60 độ, nên ta có góc MEF = góc MFA = 30 độ. Do đó, tam giác MEF là tam giác đều. Khi đó, trung trực của EF sẽ đi qua trung điểm của cạnh EF, tức là đi qua A.
b) Ta có AB là trung trực của ME và AC là trung trực của MF. Vì tam giác MEF là tam giác đều, nên EM = MF. Mà AB là trung trực của ME và AC là trung trực của MF, nên AM = BM và AM = CM. Từ đó, ta có BE + CF = BM + CM = BC.
c) Vì tam giác MEF là tam giác đều, nên góc MEF = góc MFE = góc EFM = 60 độ. Ta có góc AEF = góc MEF - góc MEA = 60 độ - 30 độ = 30 độ. Tương tự, ta có góc AFE = 30 độ.
d) Ta có AB là trung trực của ME và AC là trung trực của MF. Vì góc A = 60 độ, nên góc MEF = góc MFA = 30 độ. Khi đó, ta có góc MEF = góc MFE = 30 độ. Vì tam giác MEF là tam giác đều, nên góc EFM = góc MEF = 30 độ. Do đó, góc IMK = góc EFM = 30 độ. Ta cũng có góc AIM = góc AEM = 30 độ. Vậy MA là phân giác góc IMK.
e) Để A là trung điểm của EF, ta cần tam giác ABC là tam giác đều.
a: AB là trung trực của ME
=>AE=AM và BM=BE
AC là trung trực của MF
=>AM=AF và CM=CF
AE=AM
AM=AF
=>AE=AF
=>A nằm trên trung trực của EF
b: BE+CF
=BM+CM
=BC
c:ΔAEM cân tại A
mà AB là trung trực
nên AB là phân giác của góc EAM(1)
ΔAMF cân tại A
mà AC là đường cao
nên AC là phân giác của góc MAF(2)
Từ (1), (2) suy ra góc EAF=2*(góc BAM+góc CAM)
=>góc EAF=2*60=120 độ
ΔAEF cân tại A
=>góc AEF=góc AFE=(180-120)/2=30 độ
d: Xét ΔAEI và ΔAMI có
AE=AM
góc EAI=góc MAI
AI chung
=>ΔAEI=ΔAMI
=>góc AEI=góc AMI
Xét ΔAMK và ΔAFK có
AM=AF
góc MAK=góc FAK
AK chung
=>ΔAMK=ΔAFK
=>góc AMK=góc AFK
góc AMK=góc AFE
góc AMI=góc AEF
mà góc AFE=góc AEF
nên góc AMK=góc AMI
=>MA là phân giác của góc IMK
e: A là trung trực của EF
=>E,A,F thẳng hàng
=>góc EAF=180 độ
=>góc BAC=180/2=90 độ