Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để chứng minh ΔMAB = ΔMAC, ta có thể sử dụng nguyên lý cắt giao. Vì AB = AC và M là trung điểm BC, nên ta có AM là đường trung trực của đoạn thẳng BC. Từ đó, ta có AM ⊥ BC. Vì AM là đường trung trực của đoạn thẳng BC, nên ta cũng có MB = MC. Như vậy, ta đã chứng minh được ΔMAB = ΔMAC.
Để chứng minh AM là tia phân giác của góc BAC, ta có thể sử dụng tính chất của tam giác cân. Vì AB = AC và AM là đường trung trực của đoạn thẳng BC, nên ta có AM là tia phân giác của góc BAC.
Để chứng minh AM ⊥ BC, ta đã chứng minh ở trên rồi. Vì AM là đường trung trực của đoạn thẳng BC, nên ta có AM ⊥ BC.

Vì AB=AC=> Tam giác ABC cân tại A
+) Tam giác ABC cân tại A có AM là tpg góc BAC
=> AM đồng thời là đường cao và đường trung tuyến
a) Do AM là đường trung tuyến
=> M là trung điểm BC
b) Do AM là đường cao
=> AM\(\perp\)BC
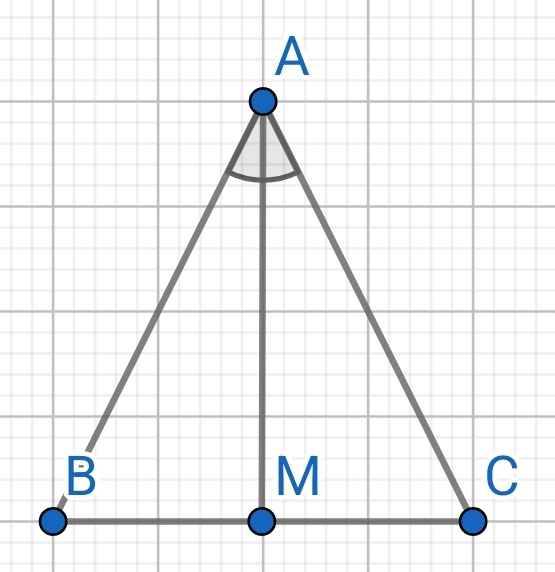 a) Do AM là tia phân giác của ∠BAC (gt)
a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AM là cạnh chung
∠BAM = ∠CAM (cmt)
AB = AC (gt)
⇒ ∆ABM = ∆ACM (c-g-c)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
b) Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC

a: Xét ΔAMB và ΔAMC có
AB=AC
AM chung
MB=MC
Do đó: ΔAMB=ΔAMC

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
b: Ta có: ΔABM=ΔACM
nên \(\widehat{BAM}=\widehat{CAM}\)
hay AM là tia phân giác của \(\widehat{BAC}\)
c: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(2)
từ (1) và (2) suy ra AM là đường trung trực của BC

\(MH\perp AB\left(gt\right)\Rightarrow\widehat{MHA}=\widehat{MHB}=90^0\)
\(MK\perp AC\left(gt\right)\Rightarrow\widehat{MKA}=\widehat{MKC}=90^0\)
M là trung điểm của BC (gt) nên MB = MC
AM là tia phân giác của góc A (gt) \(\Rightarrow\widehat{BAM}=\widehat{CAM}\Rightarrow\widehat{HAM}=\widehat{KAM}\)
\(\Delta AHM=\Delta AKM\left(ch-gn\right)\Rightarrow HM=KM\) (2 cạnh tương ứng)
\(\Delta HMB=\Delta KMC\left(ch-cgv\right)\Rightarrow\widehat{B}=\widehat{C}\) ( 2 góc t/ứ)
a) Xét \(\Delta AMC\) và \(\Delta AMB\) có:
AC = AB (gt)
CM = BM (gt,do M là trung điểm BC)
AM (cạnh chung)
Do đó \(\Delta AMC=\Delta AMB\) (c.c.c)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\Rightarrow\) M là tia phân giác của \(\widehat{BAC}\) (1)
b) \(\Delta AMC=\Delta AMB\) (chứng minh trên)
\(\Rightarrow\widehat{M_1}=\widehat{M_2}\). Mà \(\widehat{M_1} +\widehat{M_2}=180^o\) (kề bù)
Nên \(\widehat{M_1}=\widehat{M_2}=\frac{180^o}{2}=90^o\)
Suy ra \(AM\perp BC\) (2)
Từ (1) và (2) suy ra đpcm