Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC, AB<AC.Tia p/g của góc A cắt BC ở D, trên tia AC lấy điểm E sao cho AE=AB. Gọi tia M là giao điểm của AB va DE
Cmr: a) tam giác ABD=tam giacd AED
b) tam giacd DBM=tam giác DEC

Hình tự vẽ nhá
Lời giải:
trên tia AB lấy điểm N sao cho AN=AC. Do AB>AC nên N nằm giữa A và B
Vậy AB - AC = AB - AN = BN
dễ dàng chứng minh đc tam giác AEN = tam giác AEC (cgc), suy ra EN = EC (2 cạnh tương ứng)
Xét tam giác EBN có: BN > EB - EN (hệ quả của bất đẳng thức trong tam giác)
mà BN = AB - AC ( đã chứng minh)
=> AB - AC > EB - EN
lại có EN = EC (đã chứng minh), suy ra AB - AC > EB - EC ( đpcm)
ko tránh khỏi thiếu sót, nếu sai ai đó sửa lại nhé. Thắc mắc gì cứ hỏi
_Hết_

Có gì sai sót mong bạn góp ý
Trên AC lấy điểm H sao cho AH=AB
Ta có:
AH=AC-CH
Mà AH=Ab
=>AB+AC-CH
=>CH=AC-AB(1)
Xét tam giác AHE và tam giác ABE có
AH=AB(gt)
HAE=BAE
AE chung
=> Tam giác AHE=tam giác ABE(c-g-c)
=>EH=EB(2 cạnh tương ứng)
Xét tam giác EHC có
HC>EC-EH
Mà EB=EH
=>HC>EC-EB(2)
Từ (1) và (2)=>AC-AB>EC-EB

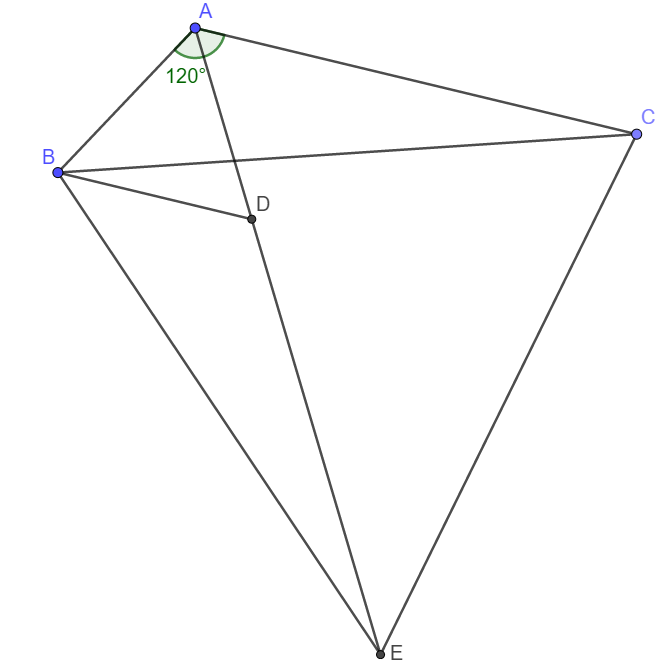
Ta có \(\widehat{BAC}=120^o\Rightarrow\widehat{BAD}=\widehat{DAC}=60^o\)
Xét tam giác ABD có AB = AD và \(\widehat{BAD}=60^o\) nên tam giác ABD đều.
Vậy thì \(\widehat{BDA}=60^o\Rightarrow\widehat{BDE}=180^o-60^o=120^o=\widehat{BAC}\)
Ta có AE = AB + AC = AD + AC
Mà AE = AD + DE nên DE = AC
Xét tam giác BAC và BDE có:
BA = BD (Do tam giác ABD đều)
AC = DE
\(\widehat{BAC}=\widehat{BDE}\)
\(\Rightarrow\Delta BAC=\Delta BDE\left(c-g-c\right)\)
\(\Rightarrow BC=BE\)
và \(\widehat{ABC}=\widehat{DBE}\Rightarrow\widehat{DBE}+\widehat{CBD}=\widehat{ABC}+\widehat{CBD}=\widehat{ABD}=60^o\)
Vậy tam giác BCE có BC = BE nên nó là tam giác cân.
Lại có \(\widehat{CBE}=60^o\) nên BCE là tam giác đều.

1/ Ta có hình vẽ:
Xét tam giác OAD và tam giác OBC có:
OA = OB (GT)
\(\widehat{O}\): góc chung
\(\begin{cases}OA=OB\\AC=BD\end{cases}\)\(\Rightarrow\)OC = OD
Vậy tam giác OAD = tam giác OBC (c.g.c)
=> AD = BC (2 cạnh tương ứng)

a) Xét tam giác ABD và tam giác AHD có:
AB = AH ( gt )
^BAD = ^CAD ( Do AD phân giác )
AD chung
=> Tam giác ABD = tam giác AHD ( c.g.c )
=> ^ABD = ^AHB ( hai góc tương ứng )
b) Xét tam giác AHE và tam giác ABC có:
AB = AH ( gt )
^ABC chung
^ABD = ^AHD ( cmt )
=> Tam giác AHE = tam giác ABC ( g.c.g )
trên AB lấy H sao cho AC = AH
xét tam giác AEC và tam giác AEH có : AE chung
^CAE = ^HAE do AE Là pg của ^BAC (Gt)
=> tam giác AEC = tam giác AEH (c-g-c)
=> EC = EH
xét tam giác EHB có HB > BE - EH
=> HB > BE - EC
có HB = AB - AH mà AH = AC (cv) => HB = AB - AC
=> AB - AC > BE - EC