K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

VT
31 tháng 12 2017
câu a, làm ở câu hỏi kia rồi
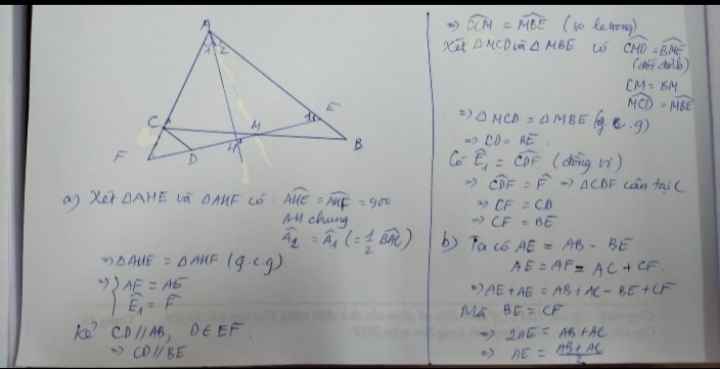
câu b) ta có
\(AE=AF\Rightarrow2AE=AE+AF=AE+AC+CF=AE+AC+BE=AB+AC\Rightarrow AE=\frac{AB+AC}{2}\left(ĐPCM\right)\)
câu c)
cái này áp dụng góc ngoài = tổng các góc trong nhé !
ta có \(\widehat{ACB}=\widehat{CFM}+\widehat{CMF}=\widehat{AEF}+\widehat{EMB}=\widehat{ABC}+\widehat{EMB}+\widehat{EMB}\Rightarrow2\widehat{EMB}=\widehat{ACB}-\widehat{ABC}\Rightarrow\frac{\widehat{ACB}-\widehat{ABC}}{2}=\widehat{EMB}\left(ĐPCM\right)\)

Thông cảm hiình hơi xấu
Kẻ CI //AB ( I thuộc EF)
xét \(\Delta BEMva\Delta CIM\) có
\(\hept{\begin{cases}MC=BM\\\widehat{MBE}=\widehat{MCI}\left(sole\right)\\\widehat{IMC}=\widehat{EMD}\left(doi-dinh\right)\end{cases}\Rightarrow\Delta BEM=\Delta CIM\left(g-c-g\right)}\)
=>BE=CI (1)
và \(\widehat{AEM}=\widehat{CIF}\) (đồng vị )
mặt khác, Xét tam giác AEF có phân giác đồng thời là đường cao => tam giác AEF cân tại A => góc AEF = góc AFE
=> góc AFE= góc CIF => tam giác CIF cân tại C => CI=CF(2)
Từ (1) và (2) => BE=CF(ĐpcM)