Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


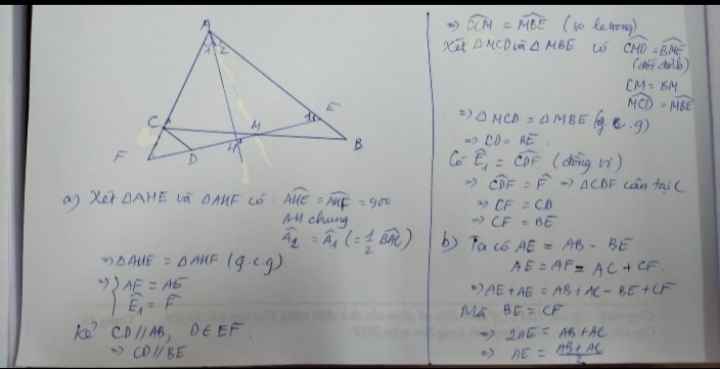
a ) AH là phân giác của \(\widehat{BAC}\)
\(\Rightarrow\widehat{EAH}=\widehat{FAH}\)
Xét 2 tam giác vuông ΔEAH và ΔFAH có:
AH chung
\(\widehat{EAH}=\widehat{FAH}\)
=> ΔEAH = ΔFAH (cạnh góc vuông - góc nhọn)
=> EH = FH (đpcm)
b ) \(\widehat{ACB}\) là góc ngoài tại C của ΔMCF
\(\Rightarrow\widehat{ACB}=\widehat{CFM}+\widehat{CMF}\)
\(\widehat{AEF}\) là góc ngoài tại E của ΔMBE
\(\Rightarrow\widehat{AEF}=\widehat{EMB}+\widehat{ABC}\)
Lại có : \(\widehat{CFM}=\widehat{AEF}\) (do ΔEAH = ΔFAH)
\(\Rightarrow\widehat{ACB}=\widehat{EMB}+\widehat{ABC}+\widehat{CMF}\)
Mặt khác \(\widehat{EMB}=\widehat{CMF}\) (đối đỉnh)
\(\Rightarrow\widehat{ACB}=2.\widehat{EMB}+\widehat{ABC}\)
Hay \(2.\widehat{BME}=\widehat{ACB}-\widehat{ABC}\)( ĐPCM )
c, ΔAHE vuông tại H
\(\Rightarrow HE^2+AH^2=AE^2\)
ΔEAH = ΔFAH ⇒ HE = HF => H là trung điểm của FE
\(\Rightarrow HE=\frac{FE}{2}\)
\(\Rightarrow HE^2=\left(\frac{FE}{2}\right)^2=\frac{FE^2}{4}\)
\(\Rightarrow\frac{FE^2}{4}+AH^2=AE^2\left(đpcm\right)\)
, Qua C kẻ đường thẳng song song với AB cắt EF ở D.
CD ║ AB \(\Rightarrow\widehat{CDF}=\widehat{AEH}\) (đồng vị)
mà \(\widehat{AFH\:}=\widehat{AEH}\)(ΔEAH = ΔFAH)
\(\Rightarrow\widehat{CDF}=\widehat{AFH\:}\)
=> ΔCDF cân tại C
=> CD = CF
Dễ dàng chứng minh được ΔMBE = ΔMCD (g.c.g)
⇒ BE = CD mà CD = CF
⇒ BE = CF (đpcm)


a, Vì AH là tia phân giác của ∠BAC
=> ∠BAH = ∠HAC = ∠BAC : 2
Xét △EAH vuong tại H và △FAH vuông tại H
Có: AH là cạnh chung
∠EAH = ∠FAH (cmt)
=> △EAH = △FAH (cgv-gn)
=> AE = AF (2 cạnh tương ứng)
Vì M là trung điểm của BC => MB = MC = BC/2
Qua C kẻ đường thẳng song song với AB cắt MF tại D
Ta có: CD // AB (cách vẽ) => ∠CDF = ∠AEF (2 góc đồng vị) (1) và ∠DCB = ∠ABC (2)
Xét △AEF có: AE = AF (cmt) => △AEF cân tại A => ∠AEF = ∠AFE (3)
Từ (1) và (3) => ∠AFE = ∠CDF hay ∠CFD = ∠CDF
Xét △CFD có: ∠CFD = ∠CDF (cmt) => △CFD cân tại C => CF = CD
Xét △CDM và △BEM
Có: ∠DCM = ∠EBM (cmt).
MC = MB (cmt)
∠CMD = ∠BME (2 góc đối đỉnh)
=> △CDM = △BEM (g.c.g)
=> CD = BE (2 cạnh tương ứng)
Mà CF = CD (cmt)
=> BE = CF
b, Ta có: AF = AC + CF (4) và AE = AB - BE (5)
Cộng 2 vế của (4) và (5) => AF + AE = AC + CF + AB - BE
Mà AF = AE và CF = BE
=> AE + AE = AC + AB
=> 2AE = AC + AB
=> AE = (AC + AB) : 2
Ta có: BE = AB - AE (6) và BE = CF mà CF = AF - AC => BE = AF - AC (7)
Cộng 2 vế của (6) và (7) => BE + BE = AB - AE + AF - AC => 2BE = AB - AC (AE = AF) => BE = (AB - AC) : 2
c, Xét △MBE có ∠MEA là góc ngoài của △ tại đỉnh E
=> ∠MEA = ∠EMB + ∠EBM => ∠AEF = ∠BME + ∠EBM => ∠AEF = ∠BME + ∠ABC
Xét △CFM có ∠MCA là góc ngoài của △ tại đỉnh C
=> ∠MCA = ∠CFM + ∠CMF => ∠ACB = ∠CFM + ∠CMF
Mà ∠CFM = ∠AEF (cmt) ; ∠CMF = ∠BME (2 góc đối đỉnh)
=> ∠ACB = ∠AEF + ∠BME
=> ∠ACB = ∠BME + ∠ABC + ∠BME
=> 2 . ∠BME + ∠ABC = ∠ACB
=> 2 . ∠BME = ∠ACB - ∠ABC
=> ∠BME = (∠ACB - ∠ABC) : 2

Một người vay 100 000 000 đồng (một trăm triệu đồng) với lãi suất 1,5% tháng. Hỏi sau 3 tháng người đó phải trả bao nhiêu tiền? (Biết lãi được nhập vốn để tính lãi tiếp tháng sau).giúp