D
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 1 2021
Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)(Tính chất đường phân giác của tam giác)
⇔\(\dfrac{4.5}{3.5}=\dfrac{7.2}{CD}\)
\(\Leftrightarrow CD=\dfrac{7.2\cdot3.5}{4.5}=5.6cm\)
Vậy: CD=5,6cm
16 tháng 3 2023
a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
b:
Sửa đề: AN=2cm
MN//BC
=>MN/BC=AN/AC
=>MN/10=2/8=1/4
=>MN=2,5cm
c AD là phân giác
=>DB/AB=DC/AC
=>DB/3=DC/4=10/7
=>DB=30/7cm; DC=40/7cm
7 tháng 4 2021
a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
7 tháng 4 2021
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15(cm)
Vậy: BC=15cm
10 tháng 3 2023
11:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot6\cdot12}{6+12}\cdot\dfrac{1}{2}=4\left(cm\right)\)
12:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot3\cdot6}{3+6}\cdot\dfrac{1}{2}=\dfrac{3\cdot6}{3+6}=\dfrac{18}{9}=2\left(cm\right)\)
D
1
24 tháng 1 2016
Có: \(\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{7}\Rightarrow BD=\frac{3}{10}BC=\frac{3}{10}.5=\frac{3}{2}=1,5\)
Vậy BD = 1,5
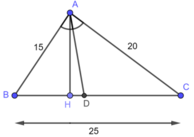
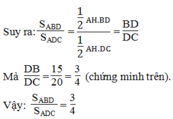
áp dụng định lí về đường phân giác của 1 góc trong tam giác . Ta có
\(\frac{AB}{AC}=\frac{DB}{DC}=\frac{3}{7}\)hay
mà DB+DC =BC=5 Ta có DB=3/10 BC
=> BD=3/10 x 5=1,5
cho **** nha