Cho tam giác ABC có A(4,-2). Đường cao BH: 2x+y-4=0 và đường cao CK: x-y-3=0. Tìm pt đi qua đỉnh A và vuông góc với cạnh...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

JE

Julian Edward

20 tháng 5 2020

Cho tam giác ABC có A(4,-2). Đường cao BH: 2x+y-4=0 và đường cao CK: x-y-3=0. Tìm pt đi qua đỉnh A và vuông góc với cạnh BC

#Toán lớp 10

1

MN

Minh Nguyệt

20 tháng 5 2020

https://i.imgur.com/mCEZa8T.jpg

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

Pham Trong Bach

11 tháng 1 2018

Cho Tam giác ABC có A( 4; -2) . Đường cao BH: 2x + y – 4= 0 và đường cao CK: x- y-3= 0. Viết phương trình đường cao kẻ từ đỉnh A. A.4x+ 5y- 6= 0 B. 4x+ 5y+ 6= 0 C. 4x- 3y+1= 0 D. 3x- 4y+ 7=...

#Toán lớp 10

1

CM

Cao Minh Tâm

11 tháng 1 2018

Đáp án A

Gọi AI là đường cao kẻ từ đỉnh A của tam giác. Gọi M là trực tâm của tam giác ABC

Khi đó tọa độ điểm M thỏa mãn hệ phương trình

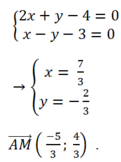
Đ ư ờ n g t h ẳ n g A I q u a M ( 7 3 ; - 2 3 ) v à n h ậ n n → ( 4 ; 5 ) l à m V T P T .

Hay 4x+ 5y – 6= 0

DN

Đặng Ngọc Đăng Thy

28 tháng 4 2020

Cho tam giác ABC có A(4;-2). Đường cao BH: 2x+y-4=0 và đường cao CK: x-y-3=0. Viết PT đường cao kẻ từ đỉnh A

#Toán lớp 10

1

NV

Nguyễn Việt Lâm

Giáo viên

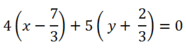
28 tháng 4 2020

Gọi I là trực tâm \(\Rightarrow\) I là giao điểm BH và CK

Tọa độ I là nghiệm: \(\left\{{}\begin{matrix}2x+y-4=0\\x-y-3=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\frac{7}{3}\\y=-\frac{2}{3}\end{matrix}\right.\)

\(\Rightarrow\overrightarrow{IA}=\left(\frac{5}{3};-\frac{4}{3}\right)=\frac{1}{3}\left(5;-4\right)\)

Đường thẳng AI nhận \(\left(4;5\right)\) là 1 vtpt

Phương trình AI:

\(4\left(x-4\right)+5\left(y+2\right)=0\Leftrightarrow4x+5y-6=0\)

TN

Thọ Nguyễn

5 tháng 5 2016

Trong mặt phẳng với hệ toạ đọ Oxy, cho tan giác ABC cân tại A, cạnh BC thuộc đường thẳng : 2x + y - 2 = 0. Đường cao BH: x + y + 1 = 0, điểm M(1;1) thuộc đường cao CK. Xác định toạ độ các đỉnh tam giác ABC.

#Toán lớp 10

0

H

huyenntranggg

3 tháng 5 2019 - olm

Cho tam giác ABC có A ( 4,2) .Đường cao BH 2x+y-4=0 vào đường cao CK x-y-3 = 0 Viết phường trình đường cao kẻ từ đỉnh A

GIÚP MÌNH VỚI MÌNH ĐANG CẦN GIẢI GẤP

#Toán lớp 10

0

PN

Phuongtrang Nguyen

10 tháng 3 2021

Cho phương trình của các cạnh và đường cao của tam giác ABC là :

AB: 2x-y+2=0; BH: x=0; AH: x-2y+1=0. Tìm A,B,C và viết phương trình đường cao CH. Tính diện tích tam giác. Tìm M,N,P đối xứng với A qua Ox, Oy và BC

#Toán lớp 10

1

HP

Hồng Phúc

12 tháng 3 2021

H là trực tâm của tam giác nhỉ.

A có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}2x-y+2=0\\x-2y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\Rightarrow A\left(-1;0\right)\)

B có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}2x-y+2=0\\x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\Rightarrow B\left(0;2\right)\)

H có tọa độ là nghiệm của hệ\(\left\{{}\begin{matrix}x-2y+1=0\\x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\end{matrix}\right.\Rightarrow H\left(0;\dfrac{1}{2}\right)\)

Phương trình đường thẳng AC: \(y=0\)

Phương trình đường thẳng CH: \(x+2y-1=0\)

C có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}y=0\\x+2y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\Rightarrow H\left(1;0\right)\)

HV

Hiếu Văn Huỳnh

18 tháng 1 2022

Trong mặt phẳng với hệ trục tọa độ Oxy, cho tam giác ABC cân tại A có BC=\(4\sqrt{2}\), các đường thẳng AB và AC lần lượt đi qua các điểm M(1,-5/3) và N(0,18/7). Xác định tọa độ các đỉnh của tam giác ABC, biết đường cao AH có pt x+y-2=0 và điểm B có hoành độ dương.

Help meee!!!

#Toán lớp 10

0

TL

🍀thiên lam🍀

11 tháng 3 2023

Cho tam giác ABC có đỉnh A(1;3), trung tuyến CE: x+y-2=0 và đường cao BH: 2x-y+3=0.

Viết phương trình AB.

_{giúp em với ạ.}

#Toán lớp 10

2

NV

Nguyễn Việt Lâm

Giáo viên

11 tháng 3 2023

Do B thuộc BH nên tọa độ có dạng \(B\left(b;2b+3\right)\)

Gọi E là trung điểm AB \(\Rightarrow E\left(\dfrac{b+1}{2};b+3\right)\)

Do E thuộc CE nên:

\(\dfrac{b+1}{2}+b+3-2=0\Rightarrow b=-1\) \(\Rightarrow B\left(-1;1\right)\)

\(\Rightarrow\overrightarrow{AB}=\left(-2;-2\right)\Rightarrow\) đường thẳng AB nhận (1;-1) là 1 vtpt

Phương trình AB:

\(1\left(x-1\right)-1\left(y-3\right)=0\Leftrightarrow x-y+2=0\)

NL

Nguyễn Lê Phước Thịnh

11 tháng 3 2023

E(x;-x+2)

Theo đề, ta có: \(\left\{{}\begin{matrix}x=\dfrac{1+x_B}{2}\\-x+2=\dfrac{3+y_B}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B+1=2x\\y_B+3=-2x+4\end{matrix}\right.\)

=>B(2x-1;-2x+1)

vecto AB=(2x-2;-2x-2)

BH: 2x-y+3=0

=>VTPT là (2;-1)

=>VTCP là (1;2)

Theo đề, ta có: 1(2x-2)+2(-2x-2)=0

=>2x-2-4x-4=0

=>-2x-6=0

=>x=-3

=>B(5;-5)

vecto AB=(4;-8)

=>VTPT là (8;4)

Phương trình AB là:

8(x-5)+4(y+5)=0

=>2(x-5)+y+5=0

=>2x-10+y+5=0

=>2x+y-5=0

HB

Hạ Băng Băng

3 tháng 2 2021

Cho tam giác ABC có 3 cạnh AB:x+y-2=0 AC:2x+3y-1=0,BC:2x-y+2=0. a, Tìm tọa độ các đỉnh của tam giác b, Tính độ dài đường cao kẻ từA c, Viết phương trình đường cao kẻ từB d, Viết phương trình đường cao kẻ từ A

#Toán lớp 10

0

PT

Pham Trong Bach

11 tháng 3 2019

Gọi H là trực tâm tam giác ABC; phương trình của các cạnh và đường cao tam giác là: AB: 7x – y+ 4= 0 và BH: 2x+ y- 4= 0; AH: x - y -2= 0 Phương trình đường cao CH của tam giác ABC là: A. 7x- y+ 2= 0 B. 7x+y-2= 0 C. x+ 7y + 2= 0 D. x+ 7y-2=...

#Toán lớp 10

1

CM

Cao Minh Tâm

11 tháng 3 2019

Hai đường thẳng AH và BH cắt nhau tại H nên tọa đô của H là nghiệm hệ

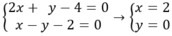
Vậy H( 2; 0)

Do CH vuông góc với AB mà AB: 7x – y + 4= 0 nên CH có

Suy ra; phương trình CH:

1(x-2) + 7( y-0) = 0

Hay x+ 7y -2= 0

Chọn D.