Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABI vuông tại I và ΔACI vuông tại I có
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Ta có: ΔABI=ΔACI
nên AB=AC
hay ΔABC cân tại A
c: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó:ABDC là hình bình hành
Suy ra: AB//CD

a) Xét tam giác(TG) AIC và tam giác EIB:
IA=IE(gt)
góc AIC= góc EIB
IC=IB(gt)
=> TG AIC= TG EIB
b) Do TG AIC = TG EIB
=> góc IAC = góc IEB(2 góc tương ứng)
mà 2 góc này ở vị trí so le trong => AC // BE
c) Xét TG IAD và TG IEK:
IA=IE(gt)
góc IAD = góc IEK(2 góc so le trong)
AD=EK(gt)
=> TG IAD = TG IEK
=> góc AID = góc EIK
mà gócAID+gócDIE=180độ
=> gócEIK+gócDIE=180độ
=> D,I,K thẳng hàng

a: Xét ΔAIC và ΔDIB có
IA=ID
ˆAIC=ˆDIBAIC^=DIB^
IC=IB
Do đó: ΔAIC=ΔDIB
Suy ra: ˆACI=ˆDBIACI^=DBI^
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
a: Xét ΔAIC và ΔDIB có
IA=ID
\(\widehat{AIC}=\widehat{DIB}\)
IC=IB
Do đó: ΔAIC=ΔDIB
b: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AC//BD
c: Ta có: AH⊥BC
DK⊥BC
Do đó: AH//DK
Xét ΔAHI vuông tại H và ΔDKI vuông tại K có
IA=ID
\(\widehat{AIH}=\widehat{DIK}\)
Do đó: ΔAHI=ΔDKI
Suy ra; AH=DK

a: Xét ΔABI và ΔACI có
AB=AC
góc BAI=góc CAI
AI chung
=>ΔABI=ΔACI
b: ΔABI=ΔACI
=>góc AIB=góc AIC
c: Xét tứ giác ABEC có
I là trung điểm chung của AE và BC
=>ABEC là hình bình hành
=>BE//AC

a: Xét ΔCIA và ΔDIB có
IC=ID
\(\widehat{CIA}=\widehat{DIB}\)
IA=IB
Do đó: ΔCIA=ΔDIB

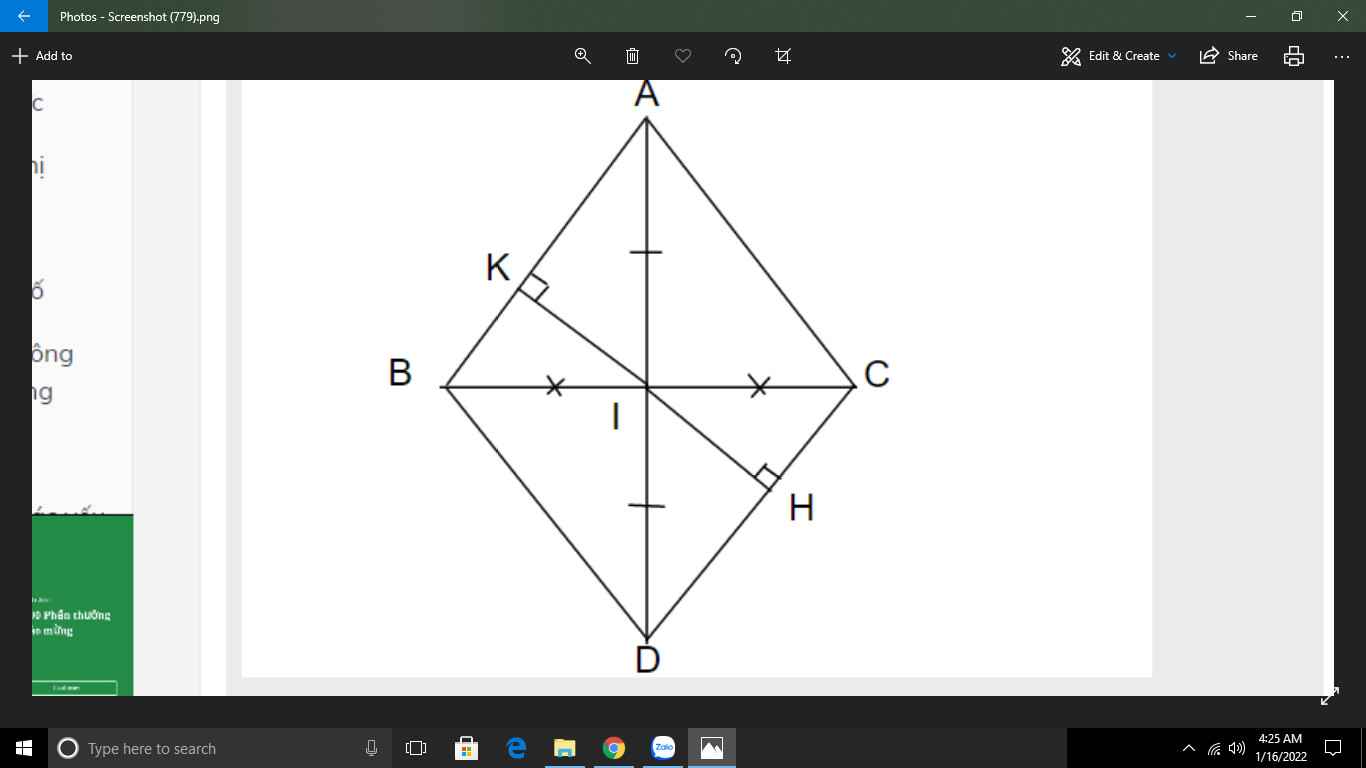
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)