Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(BH\perp AD\left(gt\right)\Rightarrow\widehat{BHA}=\widehat{BHD}=90^0\)
\(CK\perp AD\left(gt\right)\Rightarrow\widehat{AKC}=90^0\)
Xét \(\Delta BHD\)và \(\Delta CKD\) có:
\(\widehat{BHD}=\widehat{CKD}=90^0\)
\(\widehat{BDH}=\widehat{CDK}\) (đối đỉnh)
Do đó: \(\Delta BHD\infty\Delta CKD\left(g.g\right)\)
b, Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(\widehat{BAH}=\widehat{CAK}\) (vì AD là tia p/g của góc BAC)
\(\widehat{AHB}=\widehat{AKC}=90^0\)
Do đó: \(\Delta ABH\infty\Delta ACK\left(g.g\right)\)
Suy ra: \(\frac{AB}{AH}=\frac{AC}{AK}\) hay \(AB.AK=AC.AH\)
C, \(\Delta ABH\infty\Delta ACK\left(cmt\right)\Rightarrow\frac{BH}{CK}=\frac{AB}{AC}\left(1\right)\)
\(\Delta BHD=\Delta CKD\left(cmt\right)\Rightarrow\frac{DH}{DK}=\frac{BH}{CK}\left(2\right)\)
Từ (1) và (2), ta được: \(\frac{DH}{DK}=\frac{BH}{CK}=\frac{AB}{AC}\)
d, Gọi giao điểm giữa FM và BH là O và giao điểm giữa FM và CK là I.
Bạn chứng minh được tam giác BOF tại O và tam giác CIE vuông tại I
\(\Delta BOM=\Delta CIM\left(ch.gn\right)\Rightarrow BO=CI\)(2 cạnh tương ứng)
\(AD//FM\left(gt\right)\Rightarrow\hept{\begin{cases}\widehat{BAD}=\widehat{F}\\\widehat{DAC}=\widehat{IEC}\end{cases}}\)(đồng vị)
Suy ra: \(\widehat{F}=\widehat{IEC}\)
Mà \(\hept{\begin{cases}\widehat{F}+\widehat{FBO}=90^0\\\widehat{IEC}+\widehat{ICE}=90^0\end{cases}}\)
Nên \(\widehat{FBO}=\widehat{ICE}\)
Chứng minh được \(\Delta FBO=\Delta ECI\left(g.c.g\right)\Rightarrow BF=CE\)(2 cạnh tương ứng)
Chúc bạn học tốt.

H, K để làm gì?
Trog tg ADC có ME // AD => CM/CE = CD/CA (Ta-let) (1)
trog tg BMF có AD // MF => BM/BF = BD/BA (2)
theo t/c đường pg trog tg ABC có CD/CA = BD/BA (3)
Từ (1), (2) và (3) => CM/CE = BM/CF, mà CM = BM => CE = BF
Hồ sĩ tiến , để lm các câu a, b, c bn ak. Đây là câu cuối nhg mih o biết lm

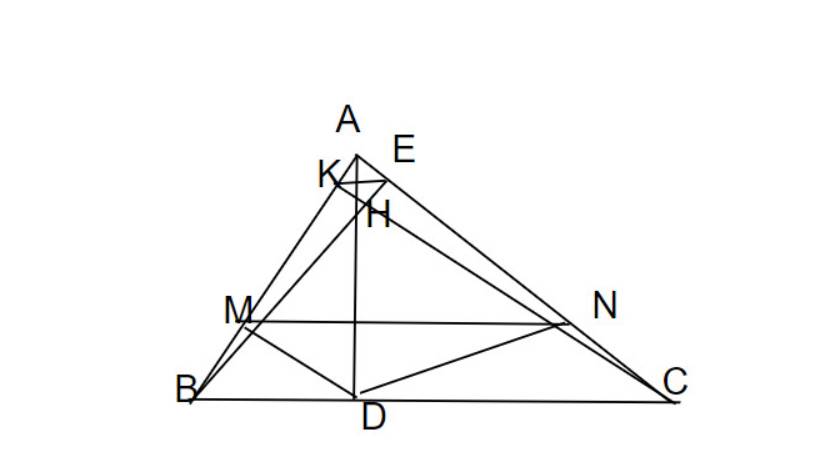
xét ΔAKH và Δ AMD, có
\(\widehat{A}=\widehat{A}\\ \widehat{K}=\widehat{M}=90^o\\ \Rightarrow\text{ }\Delta AKH\sim\Delta AMD\left(g-g\right)\)
\(\Leftrightarrow\dfrac{AH}{AD}=\dfrac{AK}{AM}\)(1)
xét ΔAKE và Δ AMN, có:
\(\widehat{A}\) chung
\(\widehat{E}=\widehat{N}\) đồng vị
\(\Rightarrow\text{ }\Delta AKE\sim\Delta AMN\left(g-g\right)\)
\(\Leftrightarrow\dfrac{AE}{AN}=\dfrac{AK}{AD}\)(2)
xét ΔAHE và Δ ADN, có:
\(\widehat{A}\) chung
từ (1) và (2) ta suy ra \(\dfrac{AH}{AD}=\dfrac{AE}{AN}\\ \Rightarrow\Delta AHE~\Delta ADN\)
\(\Leftrightarrow\widehat{E}=\widehat{N}=90^o\Rightarrow DN\perp AC\left(đpcm\right)\)
P/S: chúc bạn học tốt nhe, mình vẽ hình xong nhìn muốn nội thương=))

Xét tư giác AEDF có
DF//AE; DE//AF => AEDF là hình bình hành
Gọi O là giao của AD và EF => IA=ID và IE=IF
Xét tg AEFF có
IE=IF => AI là đường trung tuyến của tg AEF
mà AI là phân giác của \(\widehat{BAC}\)
=> tg AEF cân tại A (tg có đường trung tuyến đồng thời là đường phân giác thì tg đó là tg cân) \(\Rightarrow AD\perp EF\) (trong tg cân đường trung tuyến đồng thời là đường cao)
=> AEDF là hình thoi (Hình bh có hai đường chéo vuông góc nhau là hình thoi
=> EA=ED
Xét tg AEI và tg DEI có
EA=ED
IA=ID
EI chung
=> tg AEI=tgDEI (c.c.c) \(\Rightarrow\widehat{AEF}=\widehat{DEF}\) => EF là phân giác của \(\widehat{AED}\)


cho mình hỏi cách làm câu 1 i