Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

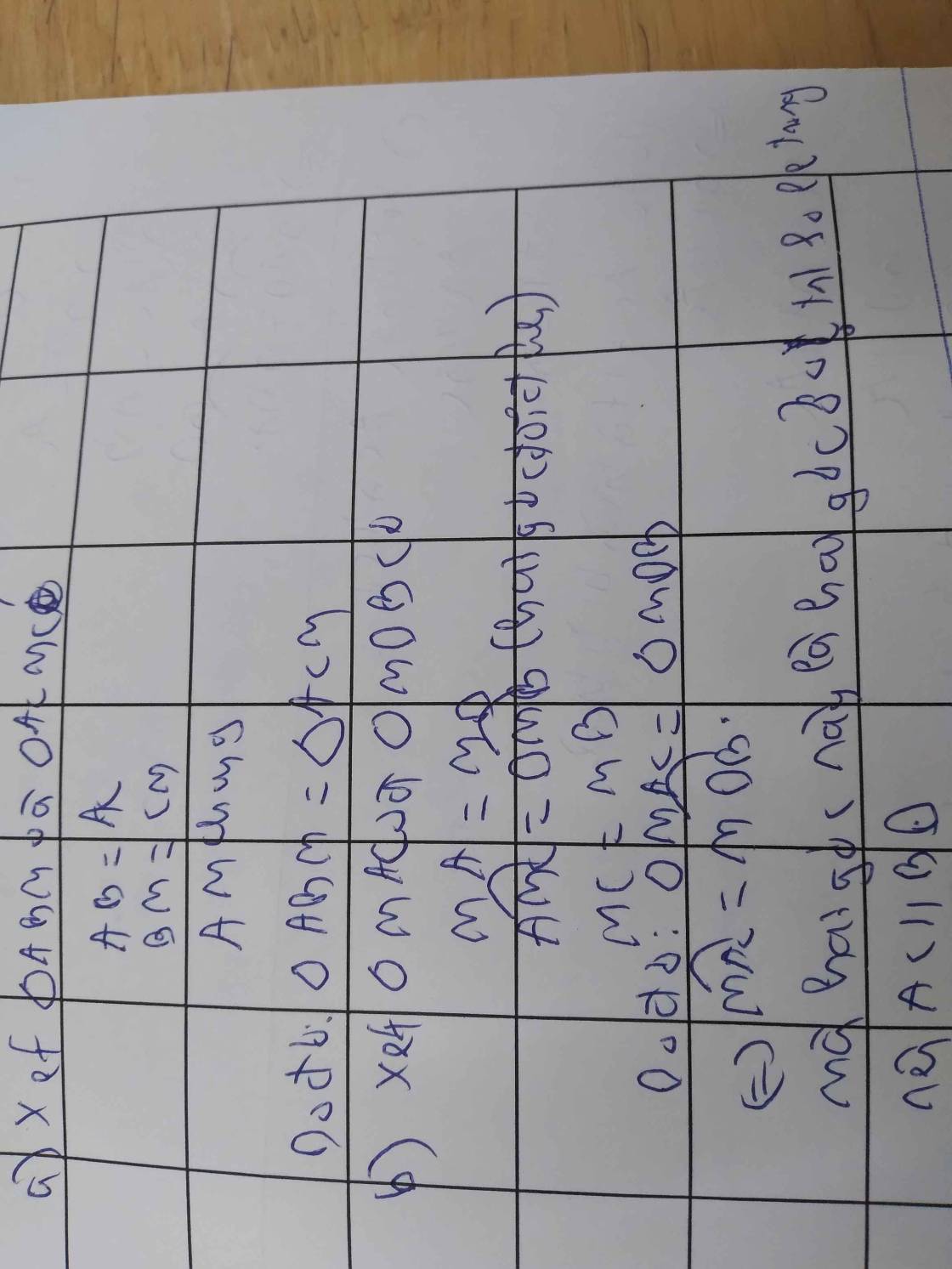
Xét tam giác ABC có
AB = AC ( = 5 cm )
=> tam giác ABC cân tại A ( ĐN)
Ta có AM là trung tuyến (gt)
=> AM là đg cao (t/c tam giác cân)
=> AM vuông BC (ĐN)
Ta có M là trung điểm của BC(AM là trung tuyến)
=> BM=CM=1/2 BC=6/2=3cm
Xét tam giác ABM có
AM vuông BC (cmt)
=> tam giác ABM vuông tại M (ĐN)
=> AM2 +BM2 = AB2 (đ/l Pitago)
Thay số: AM2 + 3 = 5
=> AM2= 5-3
=> AM2= 2
=> AM = \(\sqrt{2}\)(cm)
b) tam giác \(ABM\ne DCM\)
c) tam giác ACD ko cân

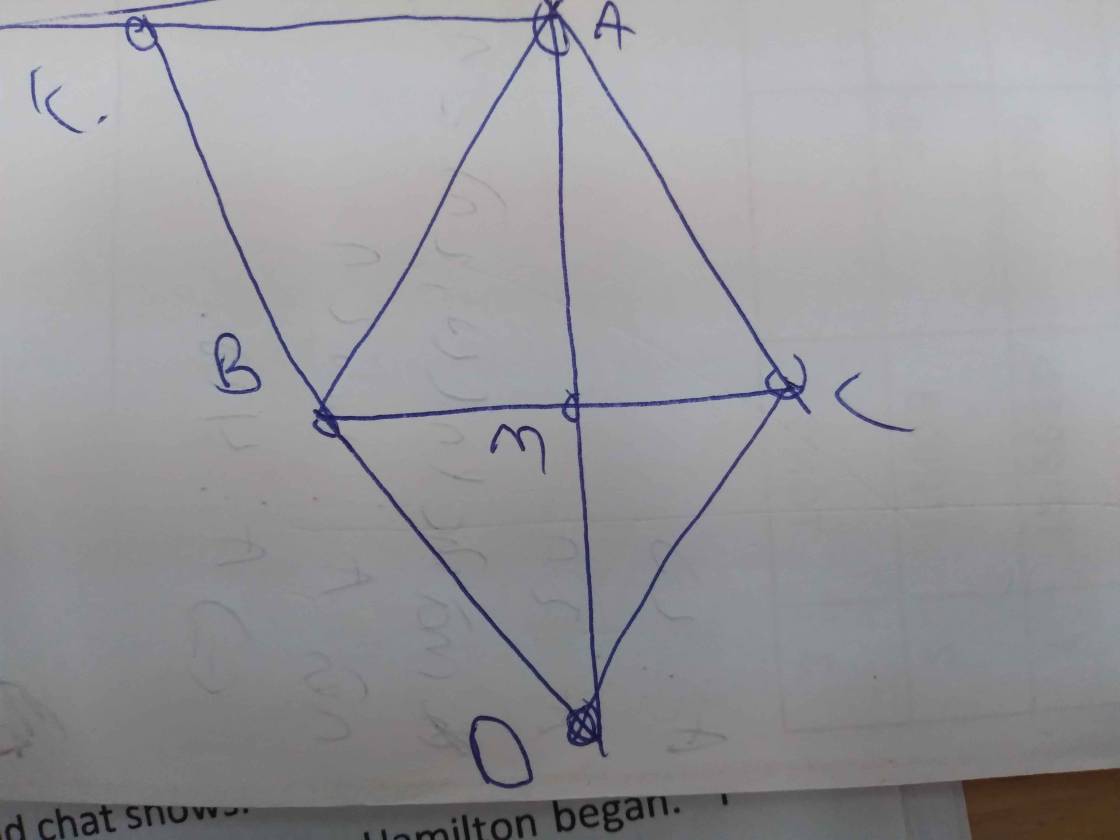
a: Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
Do đo ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
=>AC//BD
c: Xét ΔAHB vuông tại H và ΔDKC vuông tại K có
AB=DC
góc ABH=góc DCK
Do đo: ΔAHB=ΔDKC
=>AH=DK và BK=CH

Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng

a, áp dụng định lí py-ta-go ta có:
BC2 =AB2+AC2
=> AC2=BC2−AB2
=> AC2=100−36
=> AC2=64 => AC=8 cm
vậy AC=8 cm
vì BC>AC>AB(10cm>8cm>6cm)
=>\(\widehat{A}\) > \(\widehat{B}\)>\(\widehat{C}\) (góc đối diện vs cạnh lớn hơn là góc lớn hơn) đpcm
b, Xét 2 t.giác vuông BCA và DCA có:
AB=AD(gt)
AC cạnh chung
=> ΔBCA=ΔDCA(cạnh huyền -cạnh góc vuông)
=> BC=DC(2 cạnh tương ứng)
=>\(\Delta\)BCD cân tại C (đpcm)

a, áp dụng tổng 3 góc trong 1 tam giác => góc AB= 25 độ
AC < AB ( 65 độ > 25 độ)
b, Xét tam giác BHC và tam giác BHE có: BH- chung ; BHA = BHE (=90 độ) ; AH = HE ( theo đề bài)
=> hai tam giác bằng nhau (c.g.c) => BA = BE => tam giác BEA cân tại B (đpcm)
c, Dễ dàng chứng minh được tam giác BEC = tam giác BAC
=> BEC = BAC = 90 độ
=> tam giác BEC vuông tại E (đpcm)
d, Ta có: MH đi qua trung điểm của AD và AE trong tam giác ADE => NM là đường trung bình của tam giác này => MN // DE (đpcm)

a. Để chứng minh tam giác ABM bằng tam giác DCM, ta có:
Vì M là trung điểm của BC, nên BM = MC.Vì MD = MA, nên tam giác AMD là tam giác cân tại A.Từ đó, ta có AM = AD.Vì BM = MC và AM = AD, nên tam giác ABM và tam giác DCM có cạnh bằng nhau và góc tương ứng bằng nhau.Do đó, tam giác ABM bằng tam giác DCM.b. Để chứng minh AC song song và bằng BD, ta có:
Vì B là trung điểm của AC, nên AB = BC.Vì MD = MA, nên tam giác AMD là tam giác cân tại A.Từ đó, ta có AM = AD.Vì AB = BC và AM = AD, nên tam giác ABM và tam giác DCM có cạnh bằng nhau và góc tương ứng bằng nhau.Do đó, AC song song và bằng BD.c. Để chứng minh B, M, Q thẳng hàng và M trung trực AK, ta có:
Vì B là trung điểm của AC và Q là trung điểm của BC, nên BQ song song với AC và BQ = 1/2 AC.Vì M là trung điểm của BC, nên MQ song song với AC và MQ = 1/2 AC.Vì BQ song song với AC và MQ song song với AC, nên B, M, Q thẳng hàng.Vì M là trung điểm của BC, nên AM là đường trung trực của BC.Vậy, ta đã chứng minh được các phần a, b, c.
a: Xét ΔABM và ΔDCM có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC//BD và AC=BD


Sửa đề: MA=MK
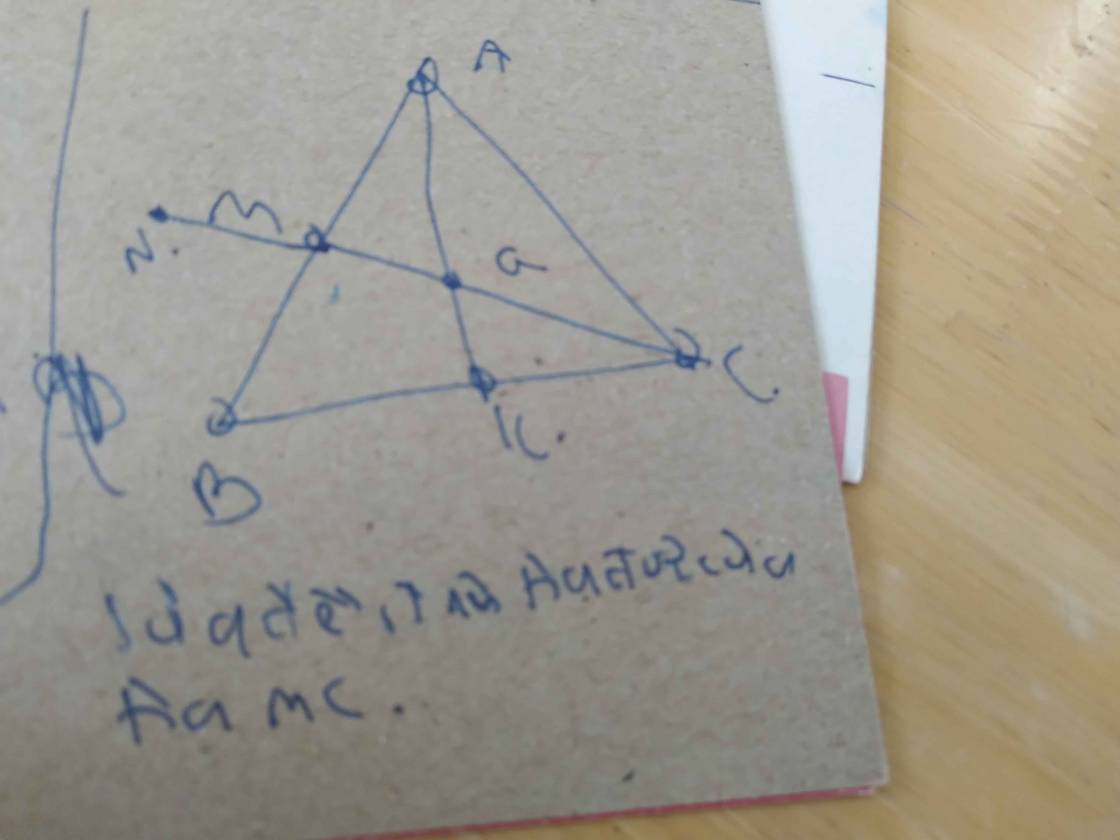
a: Xét ΔMBK và ΔMCA có
MB=MC
\(\widehat{BMK}=\widehat{CMA}\)(hai góc đối đỉnh)
MK=MA
Do đó: ΔMBK=ΔMCA
=>BK=CA
mà AB=AC
nên BK=BA
=>ΔBAK cân tại B
b: Ta có: ΔMBK=ΔMCA
=>\(\widehat{MBK}=\widehat{MCA}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BK//AC