Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các đường phân giác BD và CE cắt nhau tại K nên AK là đường phân giác của góc A.
Gọi H là trung điểm của BC
Trong tam giác cân đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời là đường trung tuyến ứng với cạnh đáy.
Vậy AK đi qua trung điểm H của BC.

a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE(cạnh huyền-góc nhọn)
Suy ra: BD=CE(hai cạnh tương ứng)
b) Ta có: ΔABD=ΔACE(cmt)
nên AD=AE(Hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)

a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE(cạnh huyền-góc nhọn)
Xét ΔBDC vuông tại D và ΔCEB vuông tại E có
BC chung
BD=CE(ΔABD=ΔACE)
Do đó: ΔBDC=ΔCEB(cạnh huyền-cạnh góc vuông)

Các đường phân giác BD và CE cắt nhau tại K nên AK la đường phân giác của góc A.
Trong một tam giác cân, đường phân giác xuất phát từ đỉnh đồng thời là đường trung tuyến, do đó AK đi qua trung điểm M của BC.

a:
BD là phân giác của \(\widehat{ABC}\)
=>\(\widehat{ABD}=\widehat{CBD}=\dfrac{1}{2}\cdot\widehat{ABC}\left(1\right)\)
CE là phân giác của \(\widehat{ACB}\)
=>\(\widehat{ACE}=\widehat{BCE}=\dfrac{1}{2}\cdot\widehat{ACB}\left(2\right)\)
ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{ABD}=\widehat{CBD}=\widehat{ACE}=\widehat{ECB}\)
Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
=>BD=CE
b: ΔABD=ΔACE
=>AD=AE
Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
nên DE//BC
c: Sửa đề: Gọi H là trung điểm của BC
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\left(cmt\right)\)
nên ΔOCB cân tại O
=>OB=OC
=>O nằm trên đường trung trực của BC(1)
AB=AC
=>A nằm trên đường trung trực của BC(2)
HB=HC
=>H nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,H thẳng hàng

Hướng dẫn :Trong 1 tam giác cân thì phân giác đồng thời là trung điểm của cạnh đối diện
Xét \(\Delta\)ABC có 2 đường phân giác là BD và CE cắt nhau tại K
=>AK là đường phân giác của góc BAC
Do: \(\Delta\)ABC cân tại A
Nên:AK đồng thời là đường trung tuyến
Vậy AK đi qua trung tuyến BC

a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>BF=CE=BD

a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>BF=CE=BD
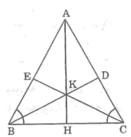



(Bạn tự vẽ hình nhé)
a/ Xét tam giác ABC có 2 đường cao BD;CE cắt nhau tại H => H là trực tâm tam giác ABC => AH là đường cao thứ 3 (=> AH vuông góc BC)
Vì tam giác ABC cân tại A => AH vừa là đường cao vừa là phân giác => góc EAH = góc DAH
Xét tam giác AEH và tam giác AHD có:
góc EAH = góc DAH (cmt)
AH: chung
góc AEH = góc ADH = 90 độ (gt)
=> tam giác AEH = tam giác ADH (g.c.g)
=> AD = AE (2 cạnh t.ứng)
b/ Vì tam giác ABC cân tại A nên AH cũng là đường trung tuyến
=> AH đi qua trung điểm BC
c/ Ta có: AE = AD (cmt)
EH = DH (vì tam giác AEH = tam giác ADH)
=> AH là đường trung trực của ED
=> AH vuông góc ED (tới đây thôi được r` dù còn 1 tính chất đường trung trực nữa. Nhưng nếu suy ra phải thêm điểm cơ)
Mà: AH vuông góc BC (gt)
=> DE // BC
10 điểm nếu vẽ hình
9 điểm giải bài