Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ΔABC cân tại A
⇒ AE là đường cao đồng thời là đường phân giác ∠BAC.
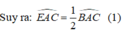
+) Tam giác ABC cân tại A nên AB = AC.
Lại có: AD = AB( giả thiết)
Suy ra: AD = AC
Do đó: ΔADC cân tại A
+) Trong tam giác ADC có: AF là đường caon nên đồng thời là đường phân giác ∠CAD.
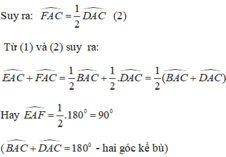

a) \(\Delta ABC\) cân tại A, AE là đường cao nên đồng thời AE là đường phân giác.
\(\Delta ACD\) cân tại A, AF là đường cao nên đồng thời là AF là đường phân giác.
AE và AF là các tia phân giác của hai góc kề bù \(\widehat{BAC},\widehat{CAD}\) nên AE \(\perp\) AF hay \(\widehat{EAF}=90^o\).


Xét tam giác ABC cân tại A có AE là đường cao ta có:
AE đồng thời là đường phân giác của tam giác.
\(\Rightarrow\widehat{BAE}=\widehat{CAE}\)
Xét tam giác ACD cân tại A có AF là đường cao ta có:
AF đồng thời là đường phân giác của tam giác.
\(\Rightarrow\widehat{CAF}=\widehat{DAF}\)
Ta có:
\(\widehat{BAC}+\widehat{DAC}=180^o\)
\(\Rightarrow\widehat{BAE}+\widehat{CAE}+\widehat{CAF}+\widehat{DAF}=180^o\)
\(\Rightarrow2\left(\widehat{CAE}+\widehat{CAF}\right)=180^o\Rightarrow\widehat{EAF}=90^o\)
Vậy...................(đpcm)
Chúc bạn học tốt!!!
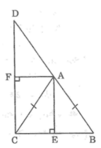


Đề thiếu. Bạn xem lại đề.