Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

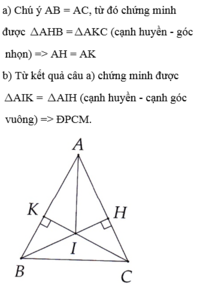
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
AK=AH
Do đó: ΔAKI=ΔAHI
Suy ra: \(\widehat{KAI}=\widehat{HAI}\)
hay AI là tia phân giác của góc BAC
c: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
d: Xét ΔABC có AK/AB=AH/AC
nên KH//BC
e: Ta có: ΔABC cân tại A
mà AI là đường phân giác
nên AI là đường cao

a, Xét \(\Delta\)tam giác vuông AKC và tam giác vuông AHB ta có :
AB=AC(do tam giácABC cân tại a)
góc A chung
=}tam giácAkc =tam giác AHB (ch_gn)
=}AH=AK(2 cạnh tương ứng)
b,Do AK=AH(cm câu a)=} I thuộc phân giác góc A
=}AI là phân giác góc A
k hộ mình nhé
a) Xét ΔACK và ΔABH
Ta có: ∠AKC = ∠AHB = 900 (gt)
AB = AC (ΔABC cân tại A)
∠BAC chung
nên ΔACK = ΔABH (cạnh huyền-cạnh góc vuông)
suy ra AH = AK
b) Ta có BH⊥AC; CK⊥AB(gt)
mà BH và CK cắt nhau tại I
nên I là trực tâm của ΔABC
suy ra AI là đường cao của ΔABC
mà ΔABC cân tại A
nên AI la Phân giác của ∠BAC

Lời giải:
a) Xét tam giác vuông $ABH$ và $ACK$ có:
$\widehat{A}$ chung
$AB=AC$ (do $ABC$ cân tại A)
$\Rightarrow \triangle ABH=\triangle ACK$ (ch-gn)
$\Rightarrow AH=AK$
b)
Xét tam giác vuông $AKI$ và $AHI$ có:$AI$ chung
$AK=AH$ (cmt)
$\Rightarrow \triangle AKI=\triangle AHI$ (ch-cgv)
$\Rightarrow \widehat{KAI}=\widehat{HAI}$ nên $AI$ là tia phân giác $\widehat{A}$