Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác ADE có góc ADE=(180 độ-góc A)/2
tương tự góc B=(180 độ-góc A)/2
=>góc B=góc ADE
mà chúng ở vị trí đồng vị nên DE//BC
tick nhan bạn

khuya rồi gửi đề dài ntn ai làm bn.....
...hỏi từng câu thôi
với lại đề copy đúng ko?(nhiều như vậy mà)
mai hỏi nha....mk ko muốn ngủ nhưng nhác trả lời^^
1. Cho tam giác ABC, D là điểm chính giữa cạnh BC, E là điểm chính giữa cạnh AC. Hai đoạn thẳng AD và BE cắt nhau tại I. Hãy so sánh diện tích tam giác AIE và BID.
CHỨNG MINH:
E là điểm giữa của AC
D là điểm giữa BC
=> ED là đường trung bình của tg ABC => ED // AB => khoảng cách từ E đến AB = khoảng cách từ D đến AB
Xét hai tg ABE và tg ABD có chung cạnh đáy AB; đường cao bằng nhau => SABE = SABD
Hai tgiác trên có phần diện tích chung là SAIB nên phần diện tích còn lại = nhau
=> SAIE = SBID
2. Cho tam giác ABC,đường cao AH = 48cm, BC = 100cm. Trên cạnh AB lấy các điểm E và D sao cho AE = ED = DB, trên cạnh AB lấy các điểm M và N sao cho AM = ED = DB, trên cạnh AC lấy các điểm M và N sao cho AM=MN=NC. Tính:
a) Diện tích tam giác ABC.
b) Diện tích tam giác BNC và tam giác BNA
c) Diện tích tam giác DEMN.
CHỨNG MINH:
a) Diện tích tg ABC là:
48 x 100 x 1/2 = 2400 (cm2)
b) Diện tích tg BNC = 1/3 diện tích tg ABC vì:
- Chung chiều cao hạ từ đỉnh B xuống AC
- Đáy NC = 1/3 AC
Diện tích tg BNC là:
2400 : 1/3 = 800 (cm2)
Diện tích tg BNA là:
2400 - 800 = 1600 (cm2)
c) Diện tích tg ABN = 2/3 ABC vì:
- Chung chiều cao hạ từ B xuống AC
- Đáy AN = 2/3 AC
Diện tích tg AEN = 1/3 ABN vì:
- Chung chiều cao hạ từ N xuống AB
- Đáy AE = 1/3 AB
Diện tích tg ANE là:
1600 x 1/3 = 1600/3 (cm2)
Diện tích tg AEM = 1/2 AEN vì:
- Chung chiều cao hạ từ E xuống AN
- Đáy AM = 1/2 AN
Diện tích tg AEM là:
1600/3 x 1/2 = 800/3 (cm2)
Diện tích hthang DEMN là:
2400 - 800 - 800/3 = 4000/3 (cm2)
:))
bài 3 chệu :((

Tam giác BDE.m là trung điểm của DE,N là trung điểm của BE => MN là đường trung bình của tam giác BDE=> MN//DB <=> MN//BA
tương tự c/m MQ là đường trung điểm của tam giác DEC => MQ//EC hay MQ//AC.Mà AC vuông góc AB=> MN vuông góc PQ => góc MNQ = 90
Tượng từ theo cách đường trung bình thì các góc còn lại của tứ giác MNPQ = 90 => là hình chữ nhạt
MN là đường trung bình => MN = 1/2 DB,MQ=1/2 EC mà EC=DB => MN=DB
=> tam giác là hình vuông (DHNB)

Bài 3:
a: Xét ΔABM và ΔACN có
AB=AC
góc ABM=góc ACN
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
Do đó; ΔAHB=ΔAKC
Suy ra: AH=AK và BH=CK
c: Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
MB=CN
góc M=góc N
Do đó ΔHBM=ΔKCN
Suy ra: góc HBM=góc KCN
=>góc OBC=góc OCB
hay ΔOBC can tại O

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).

Diện tích tam giác ABC = 60 x 30 : 2 = 900 (cm2)
Diện tích tam giác BKA = 2323 diện tích tam giác BAC
(vì cùng đường cao hạ từ B xuống AC và đáy KA = 2323AC)
Diện tích tam giác BKA là: 900×23= 600900×23= 600 (cm2)
Nối EK ta có:
Diện tích tam giác AEG = Diện tích tam giác EGK
(cùng đường cao hạ Từ E xuống AK. Đáy GA = GK)
Và diện tích tam giác KED = diện tích tam giác KDB
(Vì cùng đường cao hạ từ K xuống EB và đáy DE = DB)
Do đó:
Diện tích tam giác EGK + diện tích tam giác KED = diện tích tam giác EAG + diện tích tam giác KDB = 1212 diện tích tam giác BAK
Vậy diện tích tam giác EGK + diện tích tam giác KED = 600 : 2 = 300 (cm2)
Hay diện tích hình DEKG = 300 cm2

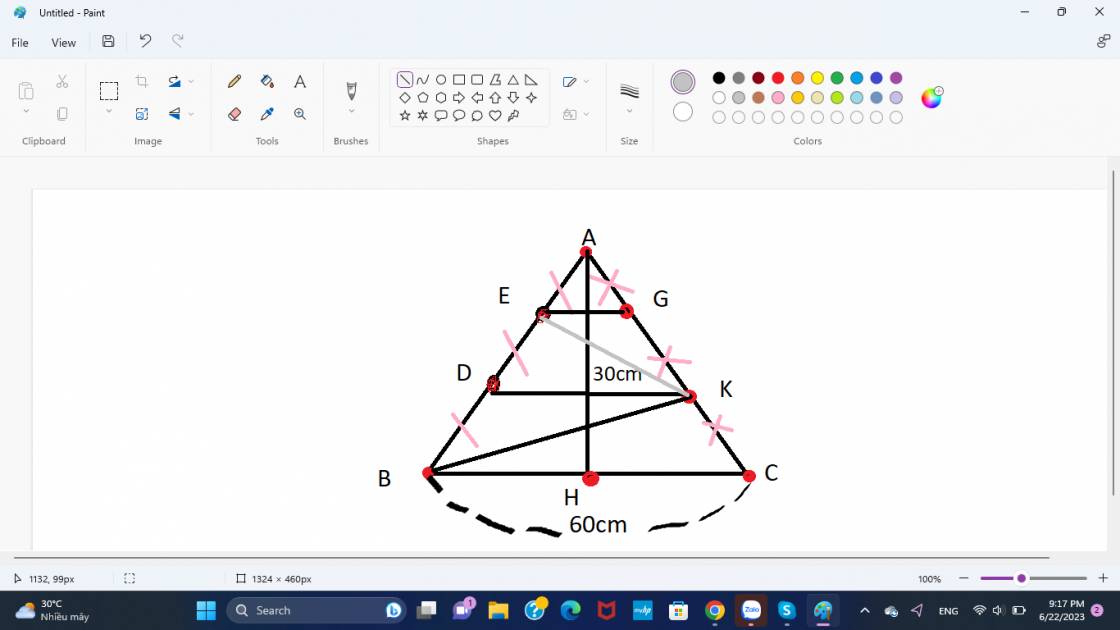
a) SABC : 60.30 :2 = 900(cm2)
b) Nối điểm E với điểm K
Ta có:
SEDK = SBDK ( vì chiều cao của 2 hình đều = \(\dfrac{1}{3}AH\) và đều hạ xuống đáy DK)
SEAG = SKDB ( vì chiều cao của 2 hình đều = \(\dfrac{1}{3}AH\) và đều hạ xuống đáy EG)
=> SEGK + SKED = SEAG + SKDB = \(\dfrac{1}{2}S_{BAK}\)
=> SDEGK = \(\dfrac{1}{2}S_{BAK}\)
\(\dfrac{S_{DEGK}}{S_{BAK}}=\dfrac{1}{2}\)