Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

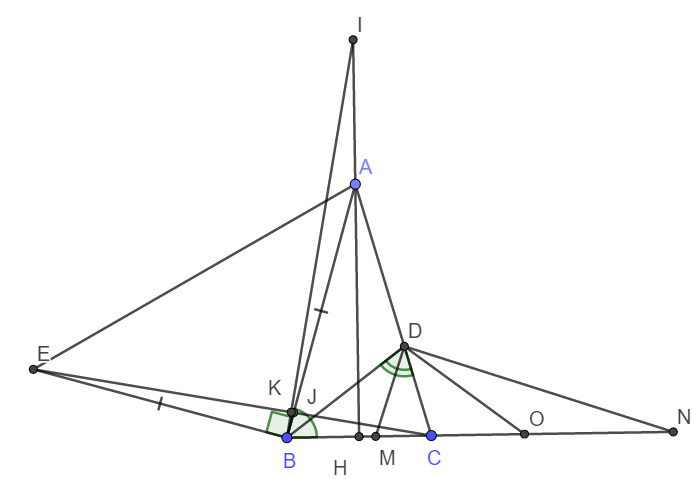
a)
+) Do tam giác ABC cân tại A nên trung tuyến AH đồng thời là đường caio.
Vậy nên \(\widehat{AHB}=90^o\)
Theo tính chất góc ngoài của tam giác, ta có:
\(\widehat{IAB}=\widehat{AHB}+\widehat{HBA}=90^o+\widehat{HBA}=\widehat{EBA}+\widehat{HBA}=\widehat{CBE}\)
Xét tam giác ABI và tam giác BEC có:
AI = BC (gt)
BA = EB (gt)
\(\widehat{IAB}=\widehat{CBE}\) (cmt)
\(\Rightarrow\Delta ABI=\Delta BEC\left(c-g-c\right)\)
+) Gọi giao điểm của EC với AB và BI lần lượt là J và K.
Do \(\Delta ABI=\Delta BEC\Rightarrow\widehat{KBJ}=\widehat{BEK}\)
Vậy thì \(\widehat{KBJ}+\widehat{KJB}=\widehat{BEK}+\widehat{KJB}=90^o\)
Suy ra \(\widehat{BKJ}=90^o\) hay \(BI\perp CE\)
b) Gọi O là trung điểm MN. Ta thấy DN và DM là phân giác của hai góc kề bù nên chúng vuông góc với nhau.
Vậy tam giác DMN vuông tại D. Khi đó ta có DO là trung tuyến ứng với cạnh huyền nên DO = MN/2
Vậy DO = OM = OM hay các tam giác DOM và DON cân tại O.
Ta có: \(\widehat{DOM}=180^o-2\widehat{DMO}=180^o-2\left(\widehat{MDB}+\widehat{MBD}\right)\)
\(=180^o-2.\widehat{MDB}-2.\widehat{MBD}=180^o-\widehat{BDC}-\widehat{ABC}\)
\(=180^o-\widehat{BDC}-\widehat{ACB}=\widehat{DBO}\)
Vậy tam giác DBO cân tại D hay DB = DO.
Vậy nên BD = MN/2.
xét tam giác BAI va CBE
be=ab
bc=ia
iab=ebc
=>tam giác BAI=tam giác CBE

Em tham khảo tại đây nhé.
Câu hỏi của Nguyễn Minh Huy - Toán lớp 7 - Học toán với OnlineMath

Câu hỏi của Nguyễn Minh Huy - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

a) Ta có: I nằm trên đường trung trực của BC(gt)
nên IB=IC(Tính chất đường trung trực của một đoạn thẳng)

a) Vẽ tia đối của BC là Bx. Gọi giao điểm của BI và CE là M. CE giao AB tại N.
\(\Delta\)ABC cân tại A. H là trung điểm của BC => AH là đường cao của \(\Delta\)ABC => AH\(⊥\)BC.
Ta có: ^ABH+^EBx=1800-^ABE=900 (1)
\(\Delta\)AHB vuông tại H => ^ABH+^BAH=900 (2)
Từ (1) và (2) => ^EBx=^BAH => 1800-^EBx=1800-^BAH => ^EBC=^BAI
Xét \(\Delta\)ABI và \(\Delta\)BEC:
AB=BE
^BAI=^EBC => \(\Delta\)ABI=\(\Delta\)BEC (c.g.c) (đpcm)
AI=BC
=> ^BEC=^ABI (2 góc tương ứng) hay ^BEN=^NBM.
\(\Delta\)EBN vuông tại B => ^BEN+^BNE=900. Thay ^BEN=^NBM, ta được:
^NBM+^BNE=900 hay ^NBM+^BNM=900. Xét \(\Delta\)BMN có:
^NBM+^BNM=900 => ^BMN=900 => BI\(⊥\)CE tại M (đpcm).

