Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


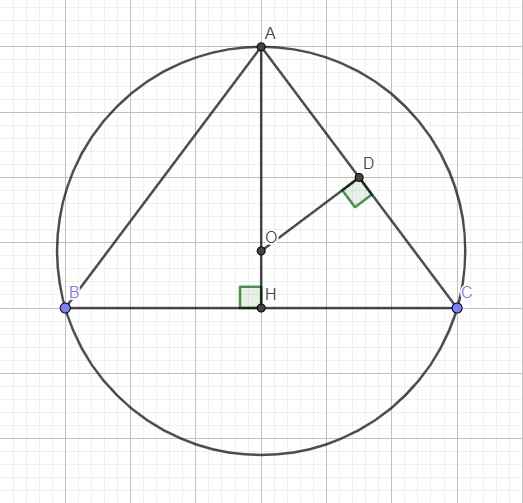
Gọi H là trung điểm BC \(\Rightarrow AH\perp BC\) và O thuộc AH do tam giác ABC cân tại A
\(CH=\dfrac{1}{2}BC=24\left(cm\right)\)
Áp dụng Pitago: \(AH=\sqrt{AC^2-CH^2}=32\left(cm\right)\)
Gọi D là trung điểm AC \(\Rightarrow\) OD là trung trực AC hay \(OD\perp AC\)
\(AD=\dfrac{1}{2}AC=20\left(cm\right)\)
Hai tam giác vuông ADO và AHC đồng dạng (chung góc A)
\(\Rightarrow\dfrac{AD}{AH}=\dfrac{AO}{AC}\Rightarrow AO=\dfrac{AD.AC}{AH}=25\left(cm\right)\)
\(\Rightarrow OH=AH-AO=7\left(cm\right)\)


Kẻ AH vuông góc với BC,suy ra AH=32 cm và A,O,H thảng hàng.
Mà AH>CH >>>O nằm giữa A và H.Kẻ OM vuông góc với AC suy ra tam giác AMO đồng dạng với AHC>>>AM/AH=AO/AC
>>>20/32=(32-OH)/40>>>OH=7cm >>>khoảng cách là 7 cm

Kẻ Đường kính AD sao cho A , O , D , H thẳng hàng .
HB = HC = BC : 2 = 24
Tam giác AHC vuông tại H , Theo py ta go tính AH
Tam giác ABD nội tiếp đường tròn tâm O đường kính AD
=> Tam giác ABD vuông tại B theo HTL tính AD
OA = AD : 2 = ....
OH = AH - OA
X=7cm
Kẻ đường cao AH, ta tính được AH = 32cm.
Do AH > HC nên tâm O nằm giữa A và H. Đặt OH = x. Kẻ OM ⊥⊥ AC.
Ta có: ΔAMO∽ΔAHCΔAMO∽ΔAHC (g.g)
⇒AOAC=AMAH⇒32−x40=2032⇒AOAC=AMAH⇒32−x40=2032.
Từ đó tính được x = 7cm.