Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo
b) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
mik tham khảo link này nha: https://lazi.vn/edu/exercise/cho-tam-giac-abc-can-tai-a-duong-cao-ah-va-trung-tuyen-bk-cat-nhau-tai-g-tia-cg-cat-ab-tai-i

Vì G là trọng tâm ΔABC
⇒AG=2323 AH=2323 18=12(cm)
Mà AG=2GH
⇒GH=AG2AG2 =122122 =6(cm)
BH=HC(do AH là trung tuyến BC)
⇒BH=HC=BC2BC2 =162162 =8(cm)
Xét ΔGHC có:
GH²+HC²=GC²(Định lí Pi-ta-go)
⇒6²+8²=GC²
⇒36+64=GC²
⇒GC²=100=10²
⇒GC=10(cm)
Mà GC=2GI
⇒GI=GC2GC2 =102102=5(cm)
Vậy độ dài cạnh GI là 5cm
d)Ta có:
Theo b) GI=GK
⇒ΔIGK là tam giác cân tại G
{GC=2GIGB=2GK{GC=2GIGB=2GK
Mà GI=GK
⇒GC=GB
⇒ΔGBC là tam giác cân tại G
Ta có:
∠KIG=∠IKG=180∗−∠IGK2180∗−∠IGK2
∠GBC=∠GCB=180∗−∠BGC2180∗−∠BGC2
Mà ∠IGK=∠BGC(đối đỉnh)
⇒∠KIG=∠GCB
Mà 2 góc ở vị trí so le trong
⇒IK=BC

Tham khảo
a.Xét ΔAHB,ΔAHC có:
Chung AHAH
ˆAHB=ˆAHC(=90o)
AB=AC
→ΔAHB=ΔAHC(cạnh huyền-cạnh góc vuông)
→HB=HC
→H là trung điểm BC
Mà K là trung điểm AC
Do AH∩BK=G
→G là trọng tâm ΔABC

a: Xét ΔABC có
AH,BK là trung tuyến
AH cắt BK tại G
=>G là trọng tâm
=>I là trung điểm của AB
=>IA=IB
c: GH=18/3=6cm
HC=16/2=8cm
=>GC=10cm
=>GI=5cm

Bạn tự vẽ hình nha!
a.
AB = AC (tam giác ABC cân tại A)
mà AB = 15 nên AC = 15
Tam giác ABC có:
AC < BC (15 < 18)
=> B < A (quan hệ giữa góc và cạnh đối diện)
b.
Xét tam giác ABH và tam giác ACH có:
A1 = A2 (AH là tia phân giác của BAC)
AB = AC (tam giác ABC cân tại A)
B = C (tam giác ABC cân tại A)
=> Tam giác ABH = Tam giác ACH (g.c.g)
c.
AH là tia phân giác của tam giác ABC cân tại A
=> AH là trung tuyến của tam giác ABC
mà BD là trung tuyến của tam giác ABC
=> G là trọng tâm của tam giác ABC.
d.
AH là tia phân giác của tam giác ABC cân tại A
=> AH là trung trực của tam giác ABC
=> H là trung điểm của BC
=> BH = CH = BC/2 = 18/2 = 9
Áp dụng định lí Pytago vào tam giác ABH vuông tại H có:
AB^2 = AH^2 + BH^2
15^2 = AH^2 + 9^2
AH = 12
Ta có:
AG = 2/3 AH (tính chất trọng tâm)
=> AG = 2/3 . 12 = 8
d.
G là trọng tâm của tam giác ABC
=> CE là trung tuyến của tam giác ABC
=> E là trung điểm của AB
=> AE = BE = AB/2
Ta có: AD = CD = AC/2 (BD là trung tuyến của tam giác ABC)
mà AB = AC (tam giác ABC cân tại A)
=> AE = AD
Xét tam giác AEG và tam giác ADG có:
AE = AD (chứng minh trên)
A1 = A2 (AH là tia phân giác của tam giác ABC)
AG là cạnh chung
=> Tam giác AEG = Tam giác ADG
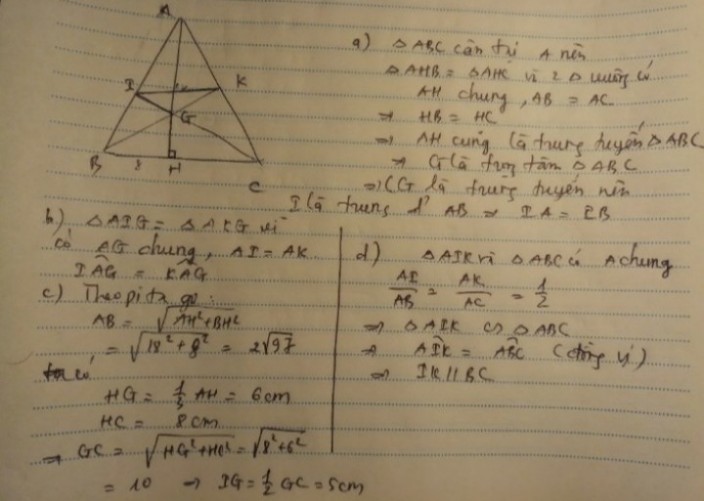
Tham khảo
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
refer
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC