Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy E sao cho A là trung điểm của CE
Xét ΔEBC có
BA là đường trung tuyến
BA=CE/2
Do đó: ΔEBC vuông tại E
Xét ΔCBE có AH//BE
nên AH/BE=CH/CB=1/2
=>AH=1/2BE
Xét ΔBEC vuông tại B có BK là đường cao
nên \(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{BE^2}\)
=>\(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)

Xét \(\Delta ACH;\Delta BCK\) có
\(\left\{{}\begin{matrix}\widehat{C}\left(chung\right)\\\widehat{AHC}=\widehat{BKC}=90^o\end{matrix}\right.\)
\(\Rightarrow\Delta ACH\sim\Delta BCK\)
\(\Rightarrow\dfrac{AH}{BK}=\dfrac{CH}{CK}\)
\(\Rightarrow AH.CK=BK.CH\)
\(\Rightarrow AH^2.CK^2=BK^2.CH^2\)
\(\Rightarrow AH^2.CK^2=\dfrac{BK^2.BC^2}{4}\)
\(\Rightarrow AH^2.\left(BC^2-BK^2\right)=\dfrac{BK^2.BC^2}{4}\)
Chia cả 2 vế cho: \(AH^2.BC^2.BK^2\)
\(\Rightarrow\dfrac{1}{BK^2}-\dfrac{1}{BC^2}=\dfrac{1}{4AH^2}\)
\(\Rightarrow\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)

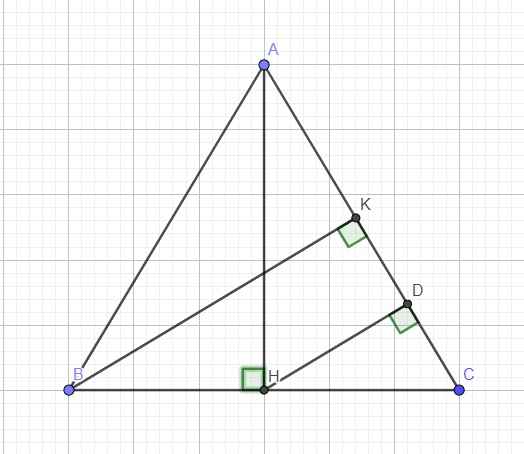
Từ H kẻ \(HD\perp AC\Rightarrow HD||BK\) (cùng vuông góc AC)
Mà ABC cân tại A \(\Rightarrow\) H là trung điểm BC \(\Rightarrow HC=\dfrac{BC}{2}\)
\(\Rightarrow\) HD là đường trung bình tam giác BCK
\(\Rightarrow HD=\dfrac{BK}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACH với đường cao HD ứng với cạnh huyền:
\(\dfrac{1}{HD^2}=\dfrac{1}{AH^2}+\dfrac{1}{CH^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{BK}{2}\right)^2}=\dfrac{1}{AH^2}+\dfrac{1}{\left(\dfrac{BC}{2}\right)^2}\)
\(\Leftrightarrow\dfrac{4}{BK^2}=\dfrac{1}{AH^2}+\dfrac{4}{BC^2}\)
\(\Leftrightarrow\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)

Do tam giác ABC cân tại A nên AH là đường cao đồng thời là trung tuyến
Hay H là trung điểm BC \(\Rightarrow CH=\dfrac{BC}{2}\)
Từ H hạ HD vuông góc AC
\(\Rightarrow HD||BK\) (cùng vuông góc AC)
\(\Rightarrow\) HD là đường trung bình tam giác ACH
\(\Rightarrow HD=\dfrac{BK}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACH:
\(\dfrac{1}{HD^2}=\dfrac{1}{AH^2}+\dfrac{1}{CH^2}\)
\(\Rightarrow\dfrac{1}{\left(\dfrac{BK}{2}\right)^2}=\dfrac{1}{AH^2}+\dfrac{1}{\left(\dfrac{BC}{2}\right)^2}\Rightarrow\dfrac{4}{BK^2}=\dfrac{1}{AH^2}+\dfrac{4}{BC^2}\)
\(\Rightarrow\dfrac{1}{BK^2}=\dfrac{1}{4AH^2}+\dfrac{1}{BC^2}\)

Lấy E sao cho A là trung điểm của CE
Xét ΔEBC có
BA là đường trung tuyến
BA=CE/2
Do đó: ΔEBC vuông tại E
Xét ΔCBE có AH//BE
nên AH/BE=CH/CB=1/2
=>AH=1/2BE
Xét ΔBEC vuông tại B có BK là đường cao
nên \(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{BE^2}\)
=>\(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)

Lấy E sao cho A là trung điểm của CE
Xét ΔEBC có
BA là đường trung tuyến
BA=CE/2
Do đó: ΔEBC vuông tại E
Xét ΔCBE có AH//BE
nên AH/BE=CH/CB=1/2
=>AH=1/2BE
Xét ΔBEC vuông tại B có BK là đường cao
nên \(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{BE^2}\)
=>\(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)

Tam giác ABC cân ở A có đường cao AH=>BC=2CH
Ta có:\(\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}=\dfrac{4AH^2+BC^2}{4BC^2AH^2}=\dfrac{4AH^2+\left(2CH\right)^2}{16S_{ABC}^2}=\dfrac{4\left(AH^2+CH^2\right)}{16S^2_{ABC}}\)
Do AH vuông góc với BC nên theo pytago AH2+CH2=AC2
=>\(\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}=\dfrac{4AC^2}{16S^2_{ABC}}=\dfrac{AC^2}{4\cdot\left(\dfrac{1}{2}AC\cdot BK\right)^2}=\dfrac{1}{BK^2}\left(ĐPCM\right)\)

Lấy E sao cho A là trung điểm của CE
Xét ΔEBC có
BA là đường trung tuyến
BA=CE/2
Do đó: ΔEBC vuông tại E
Xét ΔCBE có AH//BE
nên AH/BE=CH/CB=1/2
=>AH=1/2BE
Xét ΔBEC vuông tại B có BK là đường cao
nên \(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{BE^2}\)
=>\(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)
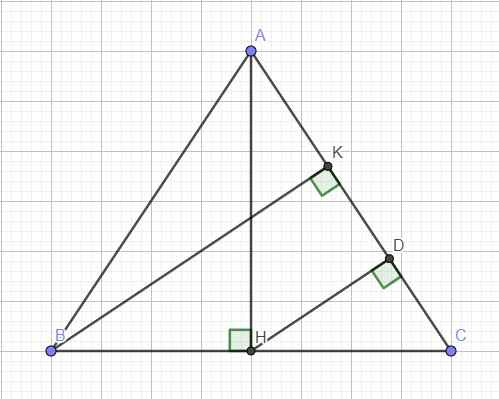

Bạn tự vẽ hình
Qua B kẻ đường thẳng song song AH cắt AC kéo dài tại D \(\Rightarrow DB\perp BC\)
\(\Rightarrow\Delta DBC\) vuông tại B
Lại có \(\Delta ABC\) cân tại A \(\Rightarrow H\) là trung điểm BC \(\Rightarrow AH\) là đường trung bình của \(\Delta DBC\Rightarrow BD=2AH\Rightarrow BD^2=4AH^2\)
Áp dụng hệ thức lượng trong tam giác vuông \(DBC\) với đường cao BK:
\(\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{BD^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\) (đpcm)