Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔAHM có
AE là đường cao
AE là đường trung tuyến
Do đó: ΔAHM cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAM(1)
Xét ΔAHN có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔAHN cân tại A
mà AC là đường cao
nên AC là tia phân giác của góc HAN(2)
Từ (1) và (2) suy ra \(\widehat{MAN}=\widehat{MAH}+\widehat{NAH}=2\cdot\widehat{BAC}=180^0\)
hay M,A,N thẳng hàng
Xét ΔAHB và ΔAMB có
AH=AM
\(\widehat{BAH}=\widehat{MAH}\)
AH chung
Do đó: ΔAHB=ΔAMB
Suy ra: \(\widehat{AHB}=\widehat{AMB}=90^0\)
hay BM\(\perp\)MA
hay BM\(\perp\)MN(3)
Xét ΔAHC và ΔANC có
AH=AN
\(\widehat{HAC}=\widehat{NAC}\)
AC chung
Do đó: ΔAHC=ΔANC
Suy ra: \(\widehat{AHC}=\widehat{ANC}=90^0\)
hay CN\(\perp\)NA
=>CN\(\perp\)NM(4)
Từ(3) và (4) suy ra MB//NC

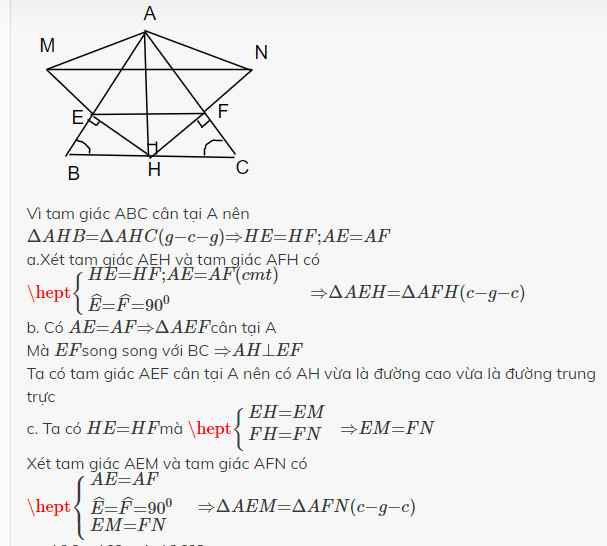
a, Xét t giác ABC cân tại A có AH là đường cao
=> AH là đường phân giác
=> góc EAH= góc FAH
xét Δ AEH và Δ AFH có
góc AEH= góc AFH = 90 độ
góc EAH= góc FAH
chung AH
=> Δ AEH = Δ AFH ( cạnh huyền - góc nhọn)
b, Xét Δ AEH = Δ AFH=> AE= AF
xét Δ AEF có AE= AF => Δ AEF cân tại A
Xét Δ AEF cân tại A có AH là đường phân giác
=> AH cũng là trung trực
=> AH là trung trực của EF (đpcm)
c, có ME= EH=> E là tđ của MH
Có AE ⊥ MH tại tđ E của MH
=> AE là trung trực của MH
=> AM= AH (1)
có FH= FN=> F là tđ của HN
Có AF ⊥ HN tại tđ F của HN
=> AF là trung trực của HN
=> AH= AN (2)
Từ (1) và (2) => AM= AN
=> Δ AMN cân tại A

Do \(AB\) là trung trực của \(HD\) nên \(AH\) nên \(AH=AD\) . Từ đó suy ra \(AB\) là phân giác góc \(DAH\) . Vậy góc \(A_1=A_2\) . Tương tự \(A_3=A_4\)
Từ đó suy ra \(A_2+A_4=A_1+A_3=90^o\)
Vậy góc \(A_1+A_2+A_3+A_4=180^o\)
Chẳng biết đúng hay sai mới chuần bị lên lớp 6
Lớp 7 chắc học đoạn thẳng tỷ lệ rùi chứ!
EG+ FH= AB
<=> EG/AB+ FH/AB = 1
áp dụng tính chất đoạn thẳng tỷ lệ, ta có:
FH/AB= CF/BC
EG/AB =CE/BC=(CF+FE)/BC
= (CF + BC - 2CF)/BC=(BC-CF)/BC = 1- CF/BC
vậy EG/AB+ FH/AB =1- CF/BC + CF/BC =1