Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


vội quá nên ẩu , toán hìh lần sau đăng sớm để giải chớ đăng hơi sát giờ tớ giải nhưng gửi ko kịp

*,tam giác HAB bằng tam giác HAC (ch-cgv) suy ra HA=HB mà AH vuông góc với BC nên AH là đương trung trực của BC
do đó:MH là đường trung trực của BC => MB=MC
*,ta có AH la đường trung tuyến của tam giác vuông nên AH= BC/2=BH (định lí)
mặt khác BH<BM(quan hệ đường xiên và đượng vuông góc)
Do đó: AH<BM
xét tam giác BMH và tam giác CMH có góc BHM= góc CHM=90 độ
BM=CM
HM là cạnh chung
=>BH=CH
=> H là trung điểm cạnh BC
Xét tam giác vuông ABC vuông tại A có H là trung điểm cạnh BC
=> AH=BH (1)
Xét tam giác BHM vông tại H => BM là cạnh lớn nhất => BM>BH (2)
Từ (1)(2)=> BM>AH

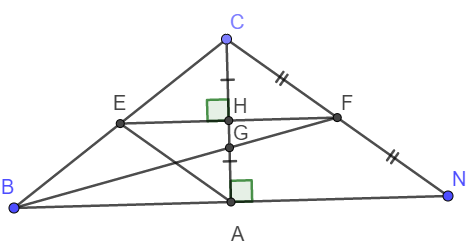
a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AC2 + AB2
252 = 152 + AB2 \(\Rightarrow ab=20\left(cm\right)\)
Xét tam giác ABC có:
AC < AB < BC nên \(\widehat{CBA}< \widehat{BCA}< \widehat{BAC}.\)
b) Xét tam giác vuông EHA và tam giác vuông EHC có:
Cạnh EH chung
HC = HA
\(\Rightarrow\Delta EHC=\Delta EHA\) (Hai cạnh góc vuông)
Do \(\Delta EHC=\Delta EHA\Rightarrow\widehat{ECA}=\widehat{EAC}\)
\(\Rightarrow\widehat{EBA}=\widehat{EAB}\) (Cùng phụ với hai góc bên trên)
Vậy nên tam giác EAB cân tại E.
c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến.
Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.
Theo tính chất trọng tâm ta có:
\(\frac{AG}{AC}=\frac{1}{3}\Rightarrow AG=\frac{1}{5}.15=5\left(cm\right)\)
d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.
Gọi giao điểm của EH với CN là F'. Khi đó ta có \(\Delta ECH=\Delta F'CH\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow CE=CF'\)
Lại có \(CE=\frac{1}{2}BC=\frac{1}{2}CN\Rightarrow CF'=\frac{1}{2}CN\)
Suy ra F' là trung điểm CN hay F' trùng F.
Vậy nên E, H, FA thẳng hàng.
Bài giải :

a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AC2 + AB2
252 = 152 + AB2 ⇒ab=20(cm)
Xét tam giác ABC có:
AC < AB < BC nên ^CBA<^BCA<^BAC.
b) Xét tam giác vuông EHA và tam giác vuông EHC có:
Cạnh EH chung
HC = HA
⇒ΔEHC=ΔEHA (Hai cạnh góc vuông)
Do ΔEHC=ΔEHA⇒^ECA=^EAC
⇒^EBA=^EAB (Cùng phụ với hai góc bên trên)
Vậy nên tam giác EAB cân tại E.
c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến.
Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.
Theo tính chất trọng tâm ta có:
AGAC =13 ⇒AG=15 .15=5(cm)
d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.
Gọi giao điểm của EH với CN là F'. Khi đó ta có ΔECH=ΔF'CH (Cạnh góc vuông và góc nhọn kề)
⇒CE=CF'
Lại có CE=12 BC=12 CN⇒CF'=12 CN
Suy ra F' là trung điểm CN hay F' trùng F.
Vậy nên E, H, FA thẳng hàng.

a, xét tam giác BMH và tam giác BDH có : BM chung
HM = HD (gt)
góc BHM = góc BHD = 90
=> tam giác BMH = tam giác BDH (2cgv)
=> BM = BD (đn)
=> tam giác BDM cân tại B (đn)
b, tam giác BMH = tam giác BDH (câu a)
=> góc MBH = góc DBH (đn)
xét tam giác BMC và tam giác BDC có : BC chung
BM = BD (câu a)
=> tam giác BMC = tam giác BMD (c - g - c)
=> góc BMC = góc BDC (đn)