NV
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
20 tháng 8 2018
Trong tam giác ABC lấy điểm M sao cho tam giác BMC đều
=> BM=CM => M thuộc trung trực cua BC
Lại có : AB=AC(ABC can tai A)
=> A thuộc trung trực cua BC
Do đó : AM là trung trực của BC
=> AM là phân giác góc BAC
=> góc MAB = góc MAC = góc BAC /2 = 20 độ/2=10 độ
tam giac ABC can tai A
=> goc CBA = goc BCA = (180 - goc BAC)/2= (180 - 20)/2 = 80 độ
lai co : goc MCA = goc ACB - goc MCB
goc MCB = 60 độ (Tg BCM đều)
Suy ra : goc MCA = 20 độ
Xet tg CMA va tg ADC co:
AC chung
CM=DA (cung bang BC)
goc MCA = goc DAC (= 20 độ)
=> tg CMA = tg ADC ( c.g.c)
=> goc CDA = goc CMA = 150 độ
Mat khac : goc CDA + goc BDC = 180 độ (2 goc ke bu)
suy ra : goc BDC = 30 độ
12 tháng 4 2019
Trong tam giác ABC lấy điểm M sao cho tam giác BMC đều
=> BM=CM => M thuộc trung trực cua BC
Lại có : AB=AC(ABC can tai A)
=> A thuộc trung trực cua BC
Do đó : AM là trung trực của BC
=> AM là phân giác góc BAC
=> góc MAB = góc MAC = góc BAC /2 = 20 độ/2=10 độ
tam giac ABC can tai A
=> goc CBA = goc BCA = (180 - goc BAC)/2= (180 - 20)/2 = 80 độ
lai co : goc MCA = goc ACB - goc MCB
goc MCB = 60 độ (Tg BCM đều)
Suy ra : goc MCA = 20 độ
Xet tg CMA va tg ADC co:
AC chung
CM=DA (cung bang BC)
goc MCA = goc DAC (= 20 độ)
=> tg CMA = tg ADC ( c.g.c)
=> goc CDA = goc CMA = 150 độ
Mat khac : goc CDA + goc BDC = 180 độ (2 goc ke bu)
suy ra : goc BDC = 30 độ
LT
11 tháng 11 2021
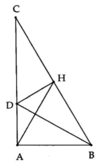
a, Xét ΔDHB và ΔDAB ta có:
HB = AB
DB chung
=> ΔDHB = ΔDAB ( cạnh huyền - cạnh góc vuông)
=> =
=> BD là tia phân giác
b, BD là tia phân giác
=> = 30
ΔABC vuông tại A có = 60
=> = 30
Xét ΔDCH và ΔDBA ta có:
= ( =30)
DH = DA ( do ΔDHA = ΔDAB chứng minh câu a)
=> ΔDCH = ΔDBA ( cạnh huyền - góc nhọn)
=> DC = DB
=> ΔBDC cân tại D
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
11 tháng 11 2021
a/ Xét tg vuông ABD và tg vuông HBD có
BD chung; HB=AB (gt) => tg ABD = tg HBD (2 tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{ABD}=\widehat{HBD}\) => BD là phân giác \(\widehat{ABC}\)
b/
Xét tg vuông ABC có
\(\Rightarrow\widehat{ACB}=90^o-\widehat{ABC}=90^o-60^o=30^o\)
\(\Rightarrow AB=\frac{BC}{2}\) (trong tg vuông cạnh đối diện với góc 30 độ bằng nửa cạnh huyền) (1)
Ta có HB=AB (gt) (2)
Từ (1) và (2) \(\Rightarrow HB=\frac{BC}{2}\) => H là trung điểm của BC => DH là trung tuyến thuộc BC
Mà \(DH\perp BC\) => DH là đường cao của tg BDC
=> tg BDC cân tại D (Trong tg nếu đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
PM
3
B2
28 tháng 8 2018
Trong tam giác ABC lấy điểm M sao cho tam giác BMC đều
=> BM=CM => M thuộc trung trực cua BC
Lại có : AB=AC(ABC can tai A)
=> A thuộc trung trực cua BC
Do đó : AM là trung trực của BC
=> AM là phân giác góc BAC
=> góc MAB = góc MAC = góc BAC /2 = 20 độ/2=10 độ
tam giac ABC can tai A
=> goc CBA = goc BCA = (180 - goc BAC)/2= (180 - 20)/2 = 80 độ
lai co : goc MCA = goc ACB - goc MCB
goc MCB = 60 độ (Tg BCM đều)
Suy ra : goc MCA = 20 độ
Xet tg CMA va tg ADC co:
AC chung
CM=DA (cung bang BC)
goc MCA = goc DAC (= 20 độ)
=> tg CMA = tg ADC ( c.g.c)
=> goc CDA = goc CMA = 150 độ
Mat khac : goc CDA + goc BDC = 180 độ (2 goc ke bu)
Suy ra : goc BDC = 30 độ
D
28 tháng 8 2018
Trong tam giác ABC lấy điểm M sao cho tam giác BMC đều.
=> BM = CM => M thuộc trung trực của BC
Lại có: AB = AC (ABC cân tại A)
=> A thuộc trung trực của BC
Do đó: AM là trung trực của BC
=> AM là phân giác góc BAC
=> Góc MAB = góc MAC = góc BAC /2 = 20 độ/2 = 10 độ
Tam giác ABC cân tại A
=> Góc CBA = góc BCA = (180 - góc BAC)/2 = (180 - 20)/2 = 80 độ
Lại có: Góc MCA = góc ACB - góc MCB
Góc MCB = 60 độ (Tg BCM đều)
Suy ra: góc MCA = 20 độ
Xét tg CMA và tg ADC có:
AC chung
CM = DA (cũng bằng BC)
Góc MCA = góc DAC (= 20 độ)
=> tg CMA = tg ADC ( c.g.c)
=> Góc CDA = góc CMA = 150 độ
Mặt khác: Góc CDA + góc BDC = 180 độ (2 góc kê bù)
Suy ra: góc BDC = 30 độ