Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AHCE có
D là trung điểm của AC
D là trung điểm của HE
Do đó: AHCE là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
b:
Sửa đề: Cắt tia EA tại M
Xét tứ giác CBMA có
CA//MB
CB//MA
Do đó: CBMA là hình bình hành
Suy ra: CM cắt BA tại trung điểm của mỗi đường
=>I là trung điểm của CM

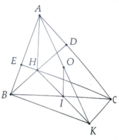
a, BHCK có I là trung điểm hai đường chéo
b, Ta có ∆ABK, ∆ACK vuông tại B và C nên A,B,K,C nằm trên đường tròn đường kính AK
c, Ta có OI là đường trung bình của ∆AHK => OI//AH
d, Gọi AH cắt BC tại M. Ta có BE.BA = BM.BC và CA.CD = CM.BC => ĐPCM

a: Xét (AH/2) có
ΔAMH nội tiếp
AH là đường kính
Do đó: ΔAMH vuông tại M
Xét (HA/2)có
ΔAHN nội tiếp
AH là đường kính
Do đó;ΔAHN vuông tại N
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
nên AMHN là hình chữ nhật
b: AM*AB=AH^2
AN*AC=AH^2
Do dó: AM*AB=AN*AC
c: góc NME
=góc NMH+góc EMH
=góc HAC+góc HCA=90 độ
=>NM là tiếp tuyến của (E)

1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.

Bạn tham khảo bài tại link :
https://olm.vn/hoi-dap/detail/244883081409.html
hoặc :
Câu hỏi của Vũ Nguyễn Phương Thảo - Toán lớp 8 - Học trực tuyến OLM
Hok tốt
a ) Tứ giác AHCE có hai đường chéo AC và HE cắt nhau tại trung điểm mỗi đường nên \(AHCE\) là hình bình hành
Lại có \(\widehat{AHC}=90^0\)
Nên tứ giác AHCE là hình chữ nhật (dấu hiệu nhận biết)
b ) Tứ giác AHCE là hình chữ nhật nên HE = AC mà AC = AB , nên HE = AB ( đpcm )
c ) \(\Delta ABC\) cân đỉnh A có AH là đường cao nên AH cũng là đường trung tuyến , nên BH = HC
\(\Rightarrow AE=BH\) ( do = HC )
Ta lại có :
AE//HC \(\Rightarrow\) AE//BH
Từ 2 điều trên suy ra ABHE là hình bình hành
\(\Rightarrow\) BF // DE ( 1 )
Tam giác ABC có 2 đường trung tuyến BD và AH giao nhau tại G nên G là trọng tâm của ΔABC
\(\Rightarrow CG\) là đường trung \(\Rightarrow F\) là trung điểm của AB
\(\Rightarrow BF=DE\left(=\frac{AB}{2}=\frac{HE}{2}\right)\left(2\right)\)
Từ (1) và (2) suy ra BDEF là hình bình hành
\(\Rightarrow\) EF // BG ( đpcm )