Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tam giác ABH và tam giác ACH vuông tại H có: +, AB = AC ( vì tam giác ABC cân tại A)
+, AH chung
=> tam giác ABH = tam giác ACH (ch-cgv) => BH = CH = 6/2 = 3cm
b, Vì BH = CH => AH là đường trung tuyến của tam giác ABC => G nằm trên AH => A, G, H thẳng hàng
c, Vì tam giác ABH = tam giác ACH => góc BAH = góc CAH
Xét tam giác ABG và tam giác ACG có
AB = AC ( vì tam giác ABC cân tại A )
góc BAH = góc CAH ( chứng minh trên)
AG chung
=>tam giác ABG = tam giác ACG(c.g.c)
=> góc ABG = góc ACG

a) Xét \(\Delta\)ABD và \(\Delta\)FBD có
BAD=BFD (=90 độ)
ABD=FBD (BD là tia pg của ABC)
BD là cạnh chung
Do đó \(\Delta\)ABD=\(\Delta\)FBD(chgn)
b)Ta có \(\Delta\)ABD=\(\Delta\)FBD(cmt)
\(\Rightarrow\)AB=FB(2 cạnh t/ứ)
\(\Rightarrow\Delta ABFcântạiB\)
Xét \(\Delta\)ABF cân tại B có : BD là pg ABC hay BD là pg ABF
\(\Rightarrow\)BD đồng thời là đường trung trực của đoạn thẳng À
c)Vì \(\Delta\) DFC vuông tại F
\(\Rightarrow\)cạnh huyền DC là cạnh lớn nhất của \(\Delta\) DFC
\(\Rightarrow\)DC>FD
Mà AD=FD (vì \(\Delta\)ABD=\(\Delta\)FBD)
Nên AD<DC
d) Xét \(\Delta\)ADE và \(\Delta\)FDC có
DAE=DFC(=90 độ)
AE=CF(gt)
AD=FD(cmt)
Do đó\(\Delta\)ADE=\(\Delta\)FDC(2 cạnh góc vuông)
\(\Rightarrow\)ADE=FDC(2 góc t./ứ)
Mà ADE+EDC=180 độ
CDF+EDC=180 độ
Hay EDF=180 độ
\(\Rightarrow\)E,D,F thẳng hàng
a)xét ΔABD và ΔFED có:
\(\widehat{BAD}=\widehat{BFD}=90^o\)
BD là cạnh chung
\(\widehat{ABD}=\widehat{FBD}\)(BD là phân giác của \(\widehat{ABF}\))
⇒ΔABD=ΔFED(c.huyền.g.nhọn)
b)gọi I là giao điểm của AF và BD
xét ΔABI và ΔFBI có:
BF=AB(ΔABD=ΔFED)
BI là cạnh chung
\(\widehat{ABI}=\widehat{FBI}\)(BD là phân giác của \(\widehat{ABF}\))
⇒ΔABI=ΔFBI(c-g-c)
⇒\(\widehat{BIA}=\widehat{BIF}\)(2 góc tương ứng)(1)
Mà \(\widehat{BIA}+\widehat{BIF}=180^o\)(2 góc kề bù)(2)
từ (1) và (2) ⇒\(\widehat{BIA}=\widehat{BIF}=\dfrac{180^o}{2}=90^o\)
vì ΔABI=ΔFBI⇒IA=IF
Do đó:BD là trung trực của AF(đ.p.cm)
c)xét ΔDCF có
DC là cạnh huyền
⇒DC>DF
Mà DF=AD
⇒DC>AD
d)Ta có:
AB=DF(ΔABD=ΔFED)
Mà AE=FC
⇒AB+AE=DF+FC
hay BE=DC
xét ΔBDC và ΔBDE có:
BE=DC(ch/m trên)
\(\widehat{EBD}=\widehat{CBD}\)(BD là phân giác của \(\widehat{EBC}\))
BD là cạnh chung
⇒ ΔBDC=ΔBDE(c-g-c)
⇒\(\widehat{BDE}=\widehat{BDC}\)(2 góc tương ứng)
Mà \(\widehat{BDA}=\widehat{BDF}\)(ΔABD=ΔFED)
⇒\(\widehat{BDE}-\widehat{BDA}=\widehat{BDC}-\widehat{BDF}\)
hay \(\widehat{ADE}=\widehat{FDC}\)(đ.p.cm)
ta có:\(\widehat{ADE}+\widehat{CDE}=180^o\)(2 góc kề bù)
Mà \(\widehat{ADE}=\widehat{FDC}\) ⇒\(\widehat{FDC}+\widehat{CDE}=180^o\)
hay E,D,F thẳng hàng(đ.p.cm)

a) Xét ΔAFC vuông tại F và ΔAFD vuông tại F có
AC=AD(=AB)
AF chung
Do đó: ΔAFC=ΔAFD(Cạnh huyền-cạnh góc vuông)
Suy ra: FC=FD(hai cạnh tương ứng)
mà C,F,D thẳng hàng(gt)
nên F là trung điểm của CD
Xét ΔBCD có
CA là đường trung tuyến ứng với cạnh BD(gt)
BF là đường trung tuyến ứng với cạnh DC(cmt)
CA cắt BF tại G(gt)
Do đó: G là trọng tâm của ΔBDC(Tính chất ba đường trung tuyến của tam giác)
\(\Leftrightarrow AG=\dfrac{1}{3}AC\)(Tính chất trọng tâm của tam giác)
mà \(AC=\dfrac{1}{2}BD\left(=AB\right)\)
nên \(AG=\dfrac{1}{3}\cdot\dfrac{1}{2}BD=\dfrac{1}{6}BD\)
hay BD=6AG(đpcm)


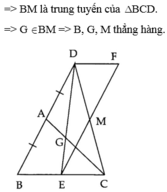
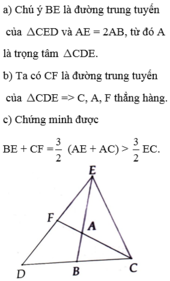
a) vì ad là trung tuyến của tam giác ABC => BC=CD
b) vì AD là trung điểm của tam giác ABC
=> BD=DC=BC/2=10/2=5
Ta có: AD^2=AB^2-BD^2
=>AD^2=144
=>AD=12
Vậy AD = 12cm
MÀ DG=1/3AD
=> DG=1/3*12=4
Vậy DG=4cm
c) Vì tam giác ABC là tam giác cân mà G là trọng tâm của tam giác ABC => A,D,G thẳng hàng
d)( mik cx ko chắc cko lắm)
Ta có: AD=12cm mà DF=DA=>DF=12cm
BD= 5cm
Vì 12cm<5cm
=> BD<CF hay CF>BD