Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 2 tam giác = nhau theo trường hợp cạnh huyền góc nhọn
b) Cx tam giác = nhau, nhiều cách
c) AH là p/giác góc A => 2 tam giác = nhau (tự chứng minh)
d) dựa vào tất cả kiến thức đã học để chứng minh
Đặng Thanh Thảo : nếu bạn gợi ý đáp án thì ít ra cx phải chi tiết hơn chứ . nói thế bạn ra đề cx bó tay .

athui mình bít vẽ oy
đọc sai đề bại
a) xét tam giác abe vuông tại e và tam giác acf vuông tại f có
ab=ac(....)
góc a chung
=> tam giác abe = tam giác acf (ch-gn)
=> be=cf( 2 cạnh tương ứng )
b) có tam giác abe = tam giác acf ( cm câu a )
=> góc abe = góc acf ( 2 góc tg ứng ) (1)
lại có tam giác abc cân tại a
=> góc acb = góc abc ( 2)
từ 1 và 2 => góc ebc = góc fcb
=> tam giác hbc cân tại h (...)
=> hb = hc ( ...)
xét tam giác fhb và tam giác ehc có
góc ech = góc fbh (...)
bh=ch (cmt)
góc fhb = góc ehc ( 2 góc đđ)
=> tam giác fhb = tam giác ehc ( g-c-g)
=> hf=he( 2 cạnh tương ứng)
=> tam giác hfe cưn tại h (...)

tự kẻ hình nha
a) xét tam giác ACF và tam giác ABE có
góc A chung
AB=AC(gt)
AFC=AEB(=90 độ)
=> tam giác ACF= tam giác ABE(ch-gnh)
CF=BE(hai cạnh tương ứng)
b) từ tam giác ACF= tam giác ABE=> AF=AE(hai cạnh tương ứng)
xét tam giác AFH và tam giác AEH có
AF=AE(cmt)
AFH=AEH(=90 độ)
AH chung
=> tam giác AFH= tam giác AE(ch-cgv)
=> FH=EH( hai cạnh tương ứng)
=> tam giác FHE cân H
c) vì AF=AE=> tam giác AFE cân A=> AFE=AEF=180-FAE/2
vì tam giác ABC cân A=> ABC=ACB=180-BAC/2
=> AFE=ACB mà AFE đồng vị với ACB => EF//BC
d) từ tam giác AFH= tam giác AEH=> A1=A2( hai góc tương ứng)
đặt O là giao điểm của AH và EF
xét tam giác AFO và tam giác AEO có
AF=AE(cmt)
A1=A2(cmt)
AO chung
=> tam giác AFO=tam giác AEO (cgc)
=> AOF=AOC( hai góc tương ứng)
mà AOF+AOC=180 độ( kề bù)
=> AOF=AOC=180/2= 90 độ=> AH vuông góc với EF

`@` `\text {dnammv}`
`a,`
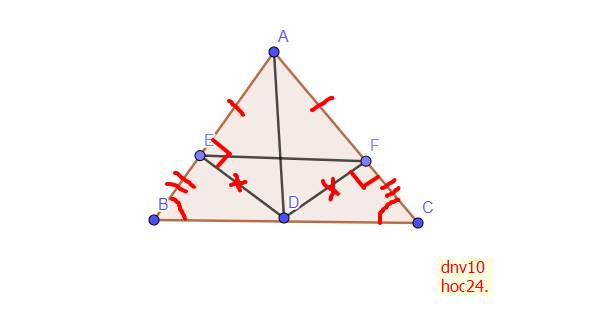
Xét \(\Delta BED\) và \(\Delta CFD\) có:
\(\left\{{}\begin{matrix}\text{BD = CD (D là trung điểm của BC}\\\widehat{\text{B}}=\widehat{\text{C}}\left(\text{ }\Delta\text{ABC cân tại A}\right)\\\widehat{BED}=\widehat{CFD}\left(=90^0\right)\end{matrix}\right.\)
`=> \Delta BED = \Delta CFD (ch-gn)`
`-> \text {BE = CF (2 cạnh tương ứng)}`
`b,`
Vì `\Delta BED = \Delta CFD (a)`
`-> \text {DE = DF (2 cạnh tương ứng)}`
`\text {Xét}` `\Delta DEF:`
`\text {DE = DF}`
`-> \Delta DEF` là `\Delta` cân
`c,`
Vì \(\left\{{}\begin{matrix}\text{AB = AC (tam giác ABC cân tại A)}\\\text{BE = CF (a)}\end{matrix}\right.\)
`-> \text {AE = AF}`
\(\text{Xét }\Delta\text{ AEF}: \)
`\text {AE = AF}`
`-> \Delta AEF` là `\Delta` cân (tại A).
`->`\(\widehat {AEF}= \widehat {AFE}\)\(=\dfrac{180-\widehat{A}}{2}\text{ }\left(1\right)\)
`\Delta ABC` cân tại `A`
`->`\(\widehat {ABC}= \widehat {ACB}=\)\(\dfrac{180-\widehat{A}}{2}\text{ }\left(2\right)\)
Từ `(1)` và `(2)`
`->`\(\widehat {AEF}= \widehat {ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {EF // BC (tính chất 2 đường thẳng //).}`
sasuke nguyên làm toán tích cực ghê, tặng bạn 2 tích nè
a,xét tam giác abe và tam giác acf có
góc aeb =góc efc
ab=ac
góc b=góc c
=>tam giác abe =tam giác acf (ch.gn)
=>be=cf