Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,
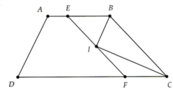
Do \(DE||BC\) (gt) \(\Rightarrow BDEC\) là hình thang
Do \(DE||BC\Rightarrow DI||BC\Rightarrow BDIC\) là hình thang
Do \(DE||BC\Rightarrow IE||BC\Rightarrow BIEC\) là hình thang
b.
Do \(DI||BC\Rightarrow\widehat{CBI}=\widehat{BID}\) (so le trong)
Mà \(\widehat{CBI}=\widehat{DBI}\) (do BI là phân giác góc B)
\(\Rightarrow\widehat{DBI}=\widehat{BID}\)
\(\Rightarrow\Delta BDI\) cân tại D
Tương tự ta có \(\widehat{ICB}=\widehat{CIE}\) (so le trong) và \(\widehat{ICB}=\widehat{ICE}\) (do IC là phân giác góc C)
\(\Rightarrow\widehat{CIE}=\widehat{ICE}\Rightarrow\Delta IEC\) cân tại E
c.
Từ câu b, do \(\Delta BDI\) cân \(\Rightarrow DB=DI\)
Do \(\Delta IEC\) cân \(\Rightarrow IE=CE\)
\(\Rightarrow BD+CE=DI+IE=DE\left(đpcm\right)\)

em tự vẽ hình
câu 1 em tự chứng minh nhé
câu 2,
ta có IE//BC\(\Rightarrow\widehat{EIC}=\widehat{ICB}\) (so le trong)
mà \(\widehat{ECI}=\widehat{ICB}\) (phân giác )
=> \(\widehat{EIC}=\widehat{ECI}\)
=> tam giác IEC cân tại E
chứng minh tương tự cvới tam giác kia nhé
c)
ta có tam giác IEC cân tại E=> IE=EC
vơi tam giác kia cân thì ta có IF=FB
=> IE+IF=BF+CE
=> EF=BF+IC

\(a,\) Các hình thang \(BDEC;BDIC;BIEC\)
\(b,DE//BC.nên.\widehat{B_1}=\widehat{I_1}\left(so.le.trong\right)\)
Mà \(\widehat{B_1}=\widehat{B_2}\left(t/c.phân.giác\right)\) nên \(\widehat{B_2}=\widehat{I_1}\Rightarrow\Delta DIB\) cân tại D
\(\Rightarrow DI=DB\left(1\right)\)
\(DE//BC.nên.\widehat{C_1}=\widehat{I_2}\left(so.le.trong\right)\)
Mà \(\widehat{C_1}=\widehat{C_2}\left(t/c.phân.giác\right)\) nên \(\widehat{C_2}=\widehat{I_2}\Rightarrow\Delta IEC\) cân tại E
\(\Rightarrow EI=EC\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow DI+IE=BD+EC\\ \Rightarrow DE=BD+CE\left(Đpcm\right)\)

b: Xét ΔDBI có
\(\widehat{DBI}=\widehat{DIB}\)
nên ΔDBI cân tại D
Xét ΔEIC có \(\widehat{EIC}=\widehat{ECI}\)
nên ΔEIC cân tại E
Ta có: DE=DI+IE
nên DE=DB+EC
Vậy: BDEC là hình thang có một cạnh đáy bằng tổng hai cạnh bên

a) HS tự tìm
b) Sử dụng các cặp góc so le trong của hai đường thẳng song song và tính chất tia phân giác.
c) Suy ra từ b)

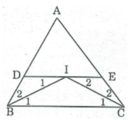
DE // BC (theo cách vẽ)
⇒ ∠ I 1 = ∠ B 1 (hai góc so le trong)
Mà ∠ B 1 = ∠ B 2 (gt)
Suy ra: ∠ I 1 = ∠ B 2
Do đó: ∆ BDI cân tại D ⇒ DI = DB (1)
Ta có: ∠ I 2 = ∠ C 1 (so le trong)
∠ C 1 = ∠ C 2 (gt)
Suy ra: ∠ I 2 = ∠ C 2 do đó: ∆ CEI cân tại E
⇒ IE = EC (2)
DE = DI + IE (3)
Từ (1), (2), (3) suy ra: DE = BD + CE
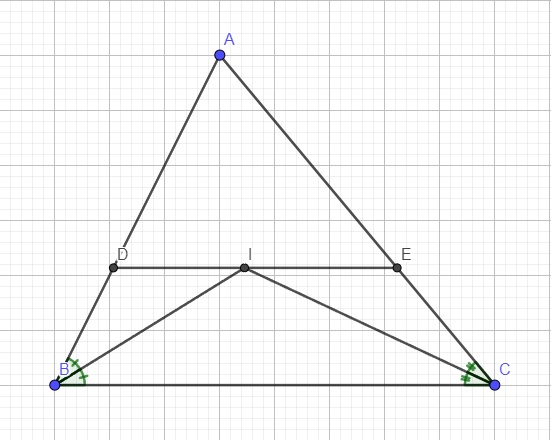
b) Ta có: \(\widehat{DBI}=\widehat{IBC}\)(gt)
mà \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
nên \(\widehat{DBI}=\widehat{DIB}\)
hay ΔDIB cân tại D
Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, IE//BC)
mà \(\widehat{ECI}=\widehat{ICB}\)(gt)
nên \(\widehat{EIC}=\widehat{ECI}\)
hay ΔEIC cân tại E
cảm ơn nha