Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AHBC có
E là trung điểm chung của AB và HC
=>AHBC là hình bình hành
Xét tứ giác ABCK có
D là trung điểm chung của AC và BK
=>ABCK là hình bình hành
b: Ta có: AHBC là hình bình hành
=>AH//BC và AH=BC
Ta có: ABCK là hình bình hành
=>AK//BC và AK=BC
Ta có: AH//BC
AK//BC
HA,AK có điểm chung là A
Do đó: H,A,K thẳng hàng
Ta có: AH=BC
AK=BC
Do đó: AH=AK
mà H,A,K thẳng hàng
nên A là trung điểm của HK

a: Xét tứ giác AHBC có
E là trung điểm chung của AB và HC
=>AHBC là hình bình hành
Xét tứ giác AKCB có
D là trung điểm chung của AC và KB
=>AKCB là hình bình hành
b:AHBC là hình bình hành
=>AH//BC và AH=BC
AKCB là hình bình hành
=>AK//CB và AK=CB
AH//BC
AK//BC
mà AH,AK có điểm chung là A
nên H,A,K thẳng hàng
AH=BC
AK=BC
Do đó: AH=AK
H,A,K thẳng hàng
mà AH=AK
nên A là trung điểm của HK

xét tg HAE và tg CEB:
HE=EC ( gt )
AE=EB (gt )
góc HEA=góc BEC ( đối đỉnh )
=> tg HAE= tg CEB ( c-g-c )
=> HA=BC ( 2 cạnh tương ứng ) ( 1)
=> góc HAE=góc EBC ( 2 góc tương ứng ) (2)
xét tương tự tg AKD và tg CBD ( tự chứng minh 2 tg bằng nhau)
=> AK= BC ( 2 cạnh tương ứng ) ( 3)
=> góc KAD= góc DCB ( 2 cạnh tương ứng ) ( 4)
từ (1) và (2) => HA=AK ( * )
từ (3) và (4 ) => góc HAE + góc BAC = góc KAD = góc ACB + góc ABC + góc BAC = 180 độ ( tổng 3 góc trog hình tg )
=> H,A,K thẳng hàng ( ** )
từ ( *) và ( ** ) => A là tđ của HK

Bài 2:
Dễ dàng chứng minh \(\Delta\)BEC = \(\Delta\)AEH (c.g.c) và \(\Delta\)CDB = \(\Delta\)ADK
Suy ra HA = BC. và KA = BC từ đó suy ra HA = KA (1)
Do ED là đường trung bình tam giác BAK nên ED // AK (2)
Do ED là đường trung bình tam giác HCA nên ED // AH (3)
Từ (2) và (3) theo tiên đề Ơclit suy ra A, H, K thẳng hàng (4)
Từ (1) và (4) suy ra đpcm.
Bài 1:
Hình như hơi dư thừa nhỉ? BHCK là hình bình hành thì hiển nhiên CH//BK rồi mà. Đúng hay sai thì tùy!
Giải
Dễ dàng chứng minh \(\Delta\)BMH = \(\Delta\)CMK (cạnh huyền - góc nhọn)
Suy ra ^MBH = ^MCK. Mà hai góc này ở vị trị so le trong nên BH // CK (1) và MH = MK
Xét \(\Delta\)BMK và \(\Delta\)CMH có:
MH = MK (chứng minh trên)
^BMK = ^HMC
BM = CM (do M là trung điểm BC)
Suy ra \(\Delta\)BMK = \(\Delta\)CMH (c.g.c)
Suy ra ^MBK = ^MCH. Mà hai góc này ở vị trí so le trong nên BK // CH (2)
Từ (1) và (2) suy ra tứ giác BHCK là hình bình hành (đpcm)

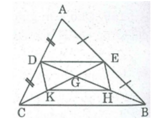
Tam giác ABC có hai đường trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm tam giác ABC.
Ta có: GD = 1/2 GB (tính chất đường trung tuyến của tam giác)
GH = 1/2 GB (gt)
Suy ra: GD = GH
GE = 1/2 GC (tính chất đường trung tuyến của tam giác)
GK = 1/2 GC
Suy ra GE = GK
Tứ giác DEHK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

\(a,\) Vì E,D là trung điểm AB,AC nên ED là đường trung bình tam giác ABC
Do đó \(ED//BC;ED=\dfrac{1}{2}BC(1)\)
Vì H,K là trung điểm GB,GC nên HK là đường trung bình tam giác BGC
Do đó \(HK//BC;HK=\dfrac{1}{2}BC(2)\)
Từ \((1)(2)\Rightarrow HK//ED;HK=ED\)
Vậy DEHK là hình bình hành
\(b,\Delta ABC\) cân tại A nên \(AB=AC\Rightarrow \dfrac{1}{2}AB=\dfrac{1}{2}AC\)
\(\Rightarrow AE=EB=AD=DC\)
Ta có \(AB=AC;AE=AD;\widehat{BAC}\) chung
\(\Rightarrow \Delta ADB=\Delta AEC(c.g.c)\\ \Rightarrow BD=EC\)
Lại có G là trọng tâm tam giác ABC nên \(CK=KG=GE=\dfrac{1}{3}CE\)
\(BH=HG=GD=\dfrac{1}{3}BD\)
Do đó \(KG+GE=HG+GD(\dfrac{2}{3}BD=\dfrac{2}{3}CE)\)
\(\Rightarrow EK=HD\)
Vậy DEHK là hình chữ nhật

Giải
Ta thấy đường trung bình tam giác ABC nên BEDC là hình thang, lại có\(BM=MC\cdot DN=NC\Rightarrow MN\) là đường trung bình hình thang BEDC hay MN ong song DE và BC. Lại dùng đường trung bình thì
\(MI=KN=\frac{DE}{2}\left(1\right)\)
\(MN=\frac{DE^2+BC}{2}\Rightarrow IK=MN-2MI=\frac{DE+BC}{2}-DE\)
\(=\frac{BC-DE}{2}=\frac{DE^2}{2}\left(BC=2DE\right)\left(2\right)\)
\(\Leftrightarrow Q\cdot E\cdot D\Rightarrowđcpm\)
![[IMG]](http://d.f10.photo.zdn.vn/upload/original/2012/07/09/20/02/1341838952939363106_574_0.jpg)
Mình sẽ làm câu b trước rồi từ đó suy ra a
b)Giả sử MP=PQ=QN đã có từ trước
Xét △△ ABC có E là trung điểm AB,D là trung điểm AC \Rightarrow ED là đường trung bình của △△ ABC\Rightarrow ED//BC và ED=BC/2(*)
Xét hình thang EDBC có M là trung điểm BE,N là trung điểm CE \Rightarrow MN//BC( (*) (*) )
Từ (*)( (*) (*) ) \Rightarrow ED//MN
Xét △△ BED có M là trung điểm BE,MP//ED \Rightarrow MP là đường trung bình của △△ BED \Rightarrow MP=ED/2
Tương tự cũng có NQ=ED/2
Ta có :MP=PQ
\Leftrightarrow ED2=BC−ED2ED2=BC−ED2
\Leftrightarrow ED=BC-ED
\Leftrightarrow 2ED=BC
Tương tự với NQ và PQ cũng rứa
Vậy muốn NQ=PQ=MP thì 2ED=BC Điều này là hiển nhiên ở (*)
từ đó phát triển lên câu a)NQ=PQ=MP=1/2ED
\Rightarrow MN=3/2ED \RightarrowMN=3/4BC
Đúng thì thanks giùm nha