

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{2+3+4}=\dfrac{180^0}{9}=20^0\\ \Rightarrow\widehat{C}=20^0.4=80^0\)
Chọn D

c) Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{B}+\widehat{C}=180^0-40^0=140^0\)
Ta có: \(\widehat{B}:\widehat{C}=3:4\)(gt)
nên \(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}\)
mà \(\widehat{B}+\widehat{C}=140^0\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{B}+\widehat{C}}{3+4}=\dfrac{140^0}{7}=20^0\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{\widehat{B}}{3}=20^0\\\dfrac{\widehat{C}}{4}=20^0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{B}=60^0\\\widehat{C}=80^0\end{matrix}\right.\)
Xét ΔABC có \(\widehat{A}< \widehat{B}< \widehat{C}\left(40^0< 60^0< 80^0\right)\)
mà cạnh đối diện với \(\widehat{A}\) là cạnh BC
cạnh đối diện với \(\widehat{B}\) là cạnh AC
và cạnh đối diện với \(\widehat{C}\) là cạnh AB
nên BC<AC<AB

Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
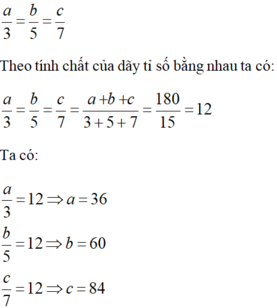
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o