Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Xét tam giác BAC và tam giác BEA ta có
^B _ chung
^BAC = ^BEA = 900
Vậy tam giác BAC ~ tam giác BEA (g.g)
b, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=25cm\)
Ta có \(S_{ABC}=\dfrac{1}{2}.AB.AC;S_{ABC}=\dfrac{1}{2}.AH.BC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{300}{25}=12cm\)
Vì BE ⊥ BD nên BE là đường phân giác góc ngoài tại đỉnh B
Suy ra :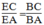 
( t/chất đường phân giác)
Suy ra: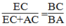 
⇒ EC.BA= BC (EC + AC)
Suy ra: EC.BA - EC.BC = BC.AC ⇒EC (BA - BC) = BC.AC
Vậy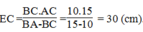 
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
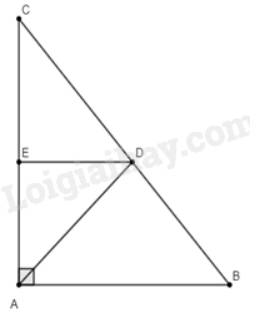
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=25/7
=>DB=75/7cm; DC=100/7cm
Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/15=100/7:25=4/7
=>DE=60/7cm
b: Xét ΔABC có BC^2=AB^2+AC^2
nen ΔABC vuông tại A
=>S ABC=1/2*15*20=10*15=150cm2
c: DB/DC=3/7
=>S ABD/S ACB=3/7
=>S ABD=150*3/7=450/7cm2
Xét \(\Delta ABC\) vuông tại A có \(AB^2+AC^2=BC^2\) (định lý Pytago)
\(\Rightarrow BC^2=12^2+16^2=20^2\Rightarrow BC=20\).
Theo tính chất đường phân giác trong tam giác ABC ta có:
\(\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{CD+BD}{AC+AB}=\dfrac{BC}{AC+AB}=\dfrac{20}{12+16}=\dfrac{5}{7}\Rightarrow BD=\dfrac{60}{7};CD=\dfrac{80}{7}\).
Ta có \(AH.BC=AB.AC\left(=2S_{ABC}\right)\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{48}{5}\).
Từ đó \(BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-\left(\dfrac{48}{5}\right)^2}=\dfrac{36}{5}\).
Suy ra \(HD=\left|BD-BH\right|=\left|\dfrac{48}{5}-\dfrac{36}{5}\right|=\dfrac{12}{5}\).
\(AD=\sqrt{AH^2+HD^2}=\dfrac{12\sqrt{17}}{5}\).
\(AC=\sqrt{12^2+16^2}=20\left(cm\right)\)
AK là phân giác
=>BK/AB=CK/AC
=>BK/3=CK/5=16/8=2
=>BK=6cm
Vì AD là đường phân giác của tam giác BAC nên ta có:
\(\dfrac{AB}{AC}=\dfrac{BD}{DC}hay\dfrac{12}{15}=\dfrac{7}{DC}\Rightarrow DC=\dfrac{12}{15}.7=5,6cm\)
Suy ra BC=BD+DC hay BC=7+5,6 \(\Rightarrow BC=12,6cm\)
Vậy BC = 12,6 cm
hình bạn tự vẽ nhá!