Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
=>ΔABE đồng dạng với ΔACF
=>AB/AC=AE/AF
=>AE/AB=AF/AC và AE*AC=AB*AF
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ACB
c; góc AFH=góc AEH=90 độ
=>AFHE nội tiếp (I)
=>IF=IE
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp (M)
=>MF=ME
=>MI là trung trực của EF
=>MI vuông góc EF

a) Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔABE∼ΔACF(g-g)
b) Ta có: ΔABE∼ΔACF(cmt)
nên \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AF\cdot AB=AE\cdot AC\)(đpcm)
c) Ta có: \(AF\cdot AB=AE\cdot AC\)(cmt)
nên \(\dfrac{AF}{AC}=\dfrac{AE}{AB}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AF}{AC}=\dfrac{AE}{AB}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔAEF∼ΔABC(c-g-c)
d) Xét ΔEBC vuông tại E và ΔDAC vuông tại D có
\(\widehat{DCA}\) chung
Do đó: ΔEBC∼ΔDAC(g-g)

a: Xét ΔBDA vuông tại D và ΔBFC vuông tại F co
góc B chung
=>ΔBDA đồng dạng vói ΔBFC
b: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AFE=góc ACB
=>ΔAFE đồng dạng vói ΔACB
c: Xét ΔAEH vuông tại E và ΔADC vuông tại D có
góc EAH chung
=>ΔAEH đồng dạng vói ΔADC
=>AD*AH=AE*AC
Xét ΔCEH vuông tại E và ΔCFA vuông tại F có
góc ECH chung
=>ΔCEH đồng dạng vói ΔCFA
=>CH*CF=CE*CA
=>AH*AD+CH*CF=CA^2

a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB∼ΔAFC(g-g)
b) Ta có: ΔAEB\(\sim\)ΔAFC(cmt)
nên \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AF\cdot AB=AE\cdot AC\)(đpcm)
Ta có: \(AF\cdot AB=AE\cdot AC\)(cmt)
nên \(\dfrac{AF}{AC}=\dfrac{AE}{AB}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AF}{AC}=\dfrac{AE}{AB}\)(cmt)
\(\widehat{FAE}\) chung
Do đó: ΔAEF\(\sim\)ΔABC(c-g-c)

3) Xét ΔFHB vuông tại F và ΔEHC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)
Do đó: ΔFHB\(\sim\)ΔEHC(g-g)
Suy ra: \(\dfrac{FH}{EH}=\dfrac{BH}{CH}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{FH}{BH}=\dfrac{EH}{CH}\)
Xét ΔFHE và ΔBHC có
\(\dfrac{FH}{BH}=\dfrac{EH}{CH}\)(cmt)
\(\widehat{FHE}=\widehat{BHC}\)(hai góc đối đỉnh)
Do đó: ΔFHE\(\sim\)ΔBHC(c-g-c)
1) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB∼ΔAFC(g-g)
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AE\cdot AC=AF\cdot AB\)(đpcm)



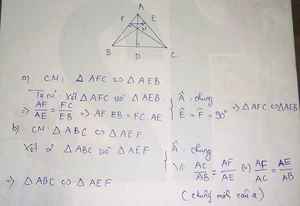
Xét \(\Delta ABE\)và \(\Delta ACF\)có:
\(\widehat{A}\)chung
\(\widehat{AEB}=\widehat{AFC\:}=90^0\)
suy ra: \(\Delta ABE~\Delta ACF\)(g.g)
\(\Rightarrow\)\(\frac{AB}{AC}=\frac{AE}{AF}\)hay \(\frac{AE}{AB}=\frac{AF}{AC}\)
Xét \(\Delta AEF\)và \(\Delta ABC\)có:
\(\frac{AE}{AB}=\frac{AF}{AC}\) (cmt)
\(\widehat{A}\) chung
suy ra: \(\Delta AEF~\Delta ABC\) (c.g.c)