Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tự kẻ hình nha
a) - Vì tam giác ABC cân tại A (gt)
=> AB = AC (định nghĩa)
góc ABC = góc ACB (dấu hiệu)
- Vì AH vuông góc với BC (gt)
=> tam giác ABH vuông tại H (tc)
tam giác ACH vuông tại H (tc)
- Xét tam giác vuông ABH và tam giác vuông ACH, có:
+ AB = AC (cmt)
+ Chung AC
=> tam giác vuông ABH = tam giác vuông ACH (cạnh huyền - cạnh góc vuông)
b) - Vì tam giác vuông ABH = tam giác vuông ACH (cmt)
=> BH = CH (2 cạnh tương ứng)
=> AH là đường trung tuyến tam giác ABC (dấu hiệu)
- Vì N là trung điểm của AC (gt)
=> BN là đường trung tuyến tam giác ABC (dấu hiệu)
Mà G là giao điểm của BN và AH (gt)
=> G là trọng tâm của tam giác ABC (tc)
- Xét tam giác ANG và tam giác CNK, có:
+ NG = NK (gt)
+ AN = CN (N là trung điểm của AC)
+ góc ANG = góc CNG (đối đỉnh)
=> tam giác ANG và tam giác CNK (cgc)
=> góc AGN = góc CKN (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=> AG // CK (dấu hiệu)
c) - Vì G là trọng tâm của tam giác ABC (cmt)
=> BG = 2/3 BN (tc)
=> NG = 1/3 BN
Mà NK = NG (gt)
=> NK = 1/3 BN
=> NK + NG = 1/3 BN + 1/3 BN
=> GK = 2/3 BN
Mà BG = 2/3 BN (cmt)
=> GK = BG
=> G là trung điểm BK

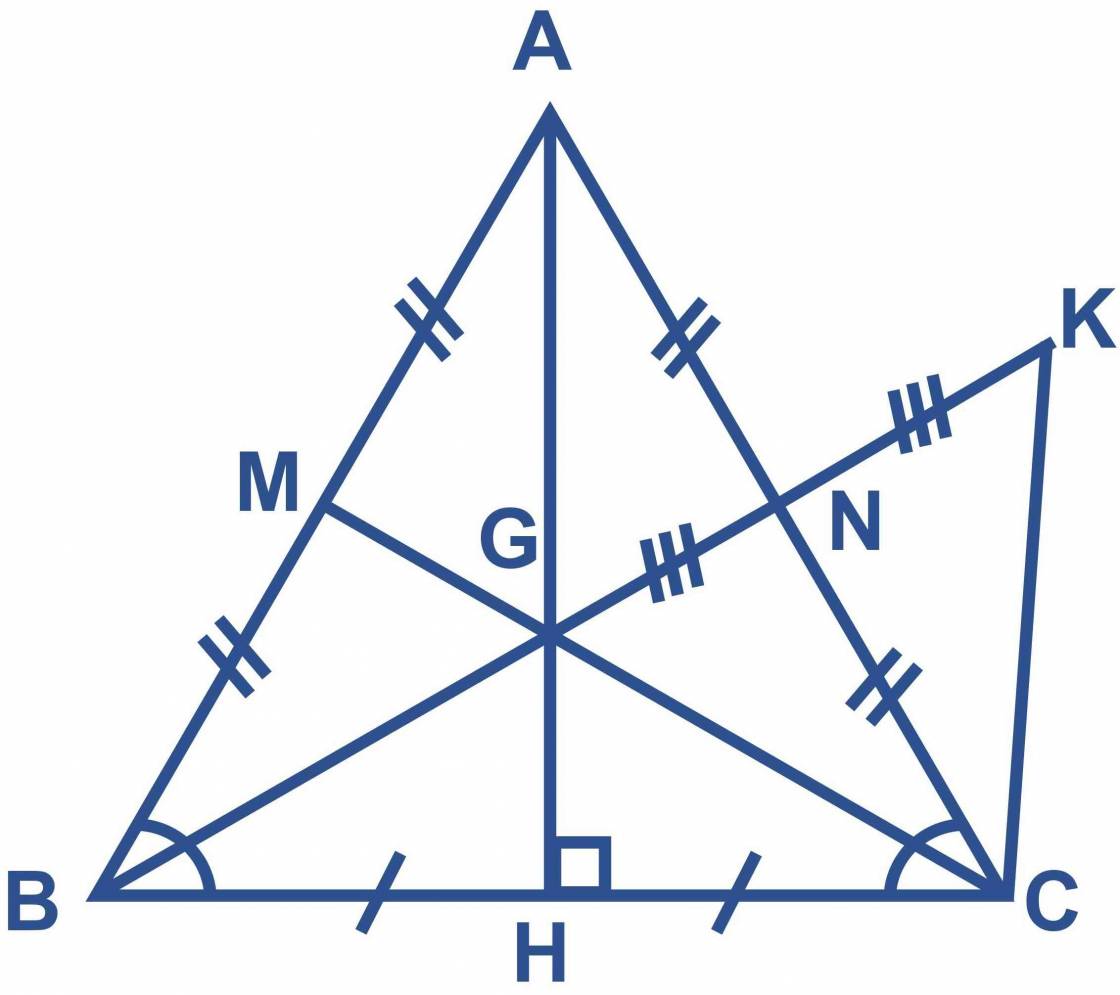
a) trong ΔABC, có góc AHB là góc vuông
góc ABH là góc nhọn
⇒ góc AHB > góc ABH
⇒ AB > AH
b) M là trung điểm của AB và N là trung điểm của AC, mà AB = AC (2 cạnh bên của tam giác cân) ⇒ MB = NC
xét tam giác MBC và tam giác NCB, ta có :
MB = NC (cmt)
góc B = góc C (2 góc đáy của 1 tam giác cân)
BC là cạnh chung
⇒ tam giác MBC = tam giác NCB (c-g-c)
⇒ MC = NB (2 cạnh tương ứng)
c) xét tam giác NAG và tam giác NCK , ta có :
NA = NC (vì N là trung điểm của cạnh AC)
góc NAG = góc NCK (đối đỉnh)
NG = NK (gt)
=> tam giác NAG = tam giác NCK (c-g-c)
=> AG = CK (2 cạnh tương ứng)

a) Ta có: \(AM=MB=\dfrac{AB}{2}\)(M là trung điểm của AB)
\(AN=NC=\dfrac{AC}{2}\)(N là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AM=MB=AN=NC
Xét ΔANB và ΔAMC có
AN=AM(cmt)
\(\widehat{BAN}\) chung
AB=AC(ΔABC cân tại A)
Do đó: ΔABN=ΔACM(c-g-c)
Suy ra: \(\widehat{ABN}=\widehat{ACM}\)(hai góc tương ứng)
hay \(\widehat{MBG}=\widehat{NCG}\)(3)
Xét ΔMBG có \(\widehat{MBG}+\widehat{MGB}+\widehat{BMG}=180^0\)(Định lí tổng ba góc trong một tam giác)(1)
Xét ΔNCG có \(\widehat{NCG}+\widehat{NGC}+\widehat{GNC}=180^0\)(Định lí tổng ba góc trong một tam giác)(2)
Từ (1), (2) và (3) suy ra \(\widehat{MGB}+\widehat{BMG}=\widehat{NGC}+\widehat{CNG}\)
mà \(\widehat{MGB}=\widehat{NGC}\)(hai góc đối đỉnh)
nên \(\widehat{BMG}=\widehat{CNG}\)
Xét ΔBMG và ΔCNG có
\(\widehat{BMG}=\widehat{CNG}\)(cmt)
BM=CN(cmt)
\(\widehat{MBG}=\widehat{NCG}\)(cmt)
Do đó: ΔBMG=ΔCNG(g-c-g)
Suy ra: GM=GN(Hai cạnh tương ứng)

( HÌNH vẽ hơi xấu )
CM
a) Xét tam giác MAI và tam giác MBC có:
\(\hept{\begin{cases}MA=MB\left(gt\right)\\\widehat{M1}=\widehat{M2}\left(2gocdoidinh\right)\\MI=MC\left(gt\right)\end{cases}\Rightarrow\Delta}MAI=\Delta MBC\left(c-g-c\right)\)
b) Xét tam giác NAK và tam giác NCB có:
\(\hept{\begin{cases}NA=NC\left(gt\right)\\\widehat{N1}=\widehat{N2}\left(2gocdoidinh\right)\\NB=NK\left(gt\right)\end{cases}}\Rightarrow\Delta NAK=\Delta NCB\left(c-g-c\right)\)
c) Vì \(\Delta MAI=\Delta MBC\left(cmt\right)\)
\(\Rightarrow\widehat{A1}=\widehat{ABC}\)( 2 góc t..ứng )
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AI//BC\left(1\right)\)
Vì \(\Delta NAK=\Delta NCB\left(cmt\right)\)
\(\Rightarrow\widehat{A2}=\widehat{ACB}\)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AK//BC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow A,I,K\)thẳng hàng ( định lý Py-ta-go )
Bạn ơi mình nhầm nhé dòng cuối cùng là theo tiên đề Ơ-clit nha xin lỗi

hình của mjnh thiếu điểm H và K rồi bạn tự thêm vào đi
a, tam giác MND cân tại M (gt)
=> ^MND = ^MDN (tc)
^MND + ^MNB = 180 (kb)
^MDN + ^MDA = 180 (kb)
=> ^MNB = ^MDA
xét tam giác MNB và tam giác MDA có BN = DA (gt)
MN = MD do tam giác MND cân tại M (gt)
=> tg MNB = tg MDA (c-g-c)
=> MA = MB (đn)
=> tg MAB cân tại M (Đn)
b, xét tam giác DHA và tam giác NKB có : AD = BN (gt)
^AHD = ^BKN = 90
^A = ^B do tam giác MAB cân tại M (câu a)
=> tg DHA = tg NKB (ch-gn)
=> DH = KN (đn)
c, tg DHA = tg NKB (câu b)
=> AH = KB (đn)
có MA = MB (câu a)
AH + MH = AM
MK + KB = BM
=> MH = MK
d, có ^HDA = ^KNB do tg DHA = tg NKB (Câu b)
^HDA = ^NDI (đối đỉnh)
^KNB = ^DNI (đối đỉnh)
=> ^NDI = ^DNI
=> tam giác DNI cân tại I
a) Xét 2 Δ KCN và Δ BAN ta có :
NA = NB (BN là trung tuyến)
Góc BNA = Góc KNC
NK = NB (đề bài)
⇒ Δ KCN = Δ BAN (cạnh, góc, cạnh)
b) Góc ABN = Góc NCK ( vì Δ KCN = Δ BAN)
mà 2 góc trên ở vị trí so le trong
⇒ AB \(//\) KC
mà AB \(\perp\) AC
⇒ KC \(//\) AC
c) Ta có : \(\dfrac{GK}{NK}=\dfrac{2}{3}\) \(\left(GK=\dfrac{2}{3}NK\right)\)
mà KN là trung tuyến Δ ACK (BN là trung tuyến ⇒ N là trung điểm AC)
⇒ G là trọng tâm của Δ ACK
mà CI là trung tuyến Δ ACK (I là trung điểm AK)
⇒ CI sẽ đi qua trọng tâm G
⇒ C, G, I thẳng hàng