Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

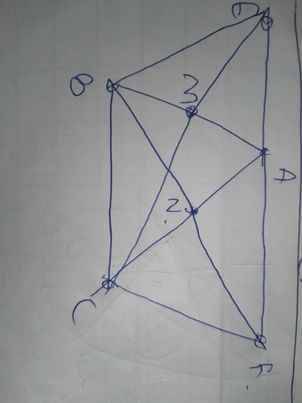
Ta có hình vẽ:
a) Vì M là trung điểm của AB nên AM = BM = \(\frac{AB}{2}\)
Xét Δ AMK và Δ BMC có:
AM = BM (cmt)
AMK = BMC (đối đỉnh)
MK = MC (gt)
Do đó, Δ AMK = Δ BMC (c.g.c) (đpcm)
b) Vì N là trung điểm của AC nên AN = NC
Xét Δ ANI và Δ CNB có:
AN = NC (cmt)
ANI = CNB (đối đỉnh)
NI = NB (gt)
Do đó, Δ ANI = Δ CNB (c.g.c)
=> AI = BC (2 cạnh tương ứng) (đpcm)
c) Vì Δ AMK = Δ BMC (câu a) => AKM = MCB (2 góc tương ứng)
Mà AKM và MCB là 2 góc so le trong nên AK // BC (1)
Vì Δ ANI = Δ CNB (câu b) => IAN = NBC (2 góc tương ứng)
Mà IAN và NBC là 2 góc so le trong nên AI // BC (2)
Từ (1) và (2) => AK và AI trùng nhau hay 3 điểm I, A, K thẳng hàng (3)
Có: Δ AMK = Δ BMC (câu a) => AK = BC (2 cạnh tương ứng)
Mà AI = BC (câu b) => AK = AI (4)
Từ (3) và (4) => A là trung điểm của IK (đpcm)

a: Xét ΔANE và ΔCNB có
NA=NC
\(\widehat{ANE}=\widehat{CNB}\)
NE=NB
Do đó: ΔANE=ΔCNB
Suy ra: \(\widehat{AEN}=\widehat{CBN}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
b: Xét ΔAMD và ΔBMC có
MA=MB
\(\widehat{AMD}=\widehat{BMC}\)
MD=MC
Do đó: ΔAMD=ΔBMC

a: Xét ΔAME và ΔBMC có
MA=MB
\(\widehat{AME}=\widehat{BMC}\)(hai góc đối đỉnh)
ME=MC
Do đó: ΔAME=ΔBMC
b: Xét ΔAFN và ΔCBN có
NA=NC
\(\widehat{ANF}=\widehat{CNB}\)(hai góc đối đỉnh)
NF=NB
Do đó: ΔAFN=ΔCBN
c: ΔAME=ΔBMC
=>\(\widehat{MAE}=\widehat{MBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
d: ΔAME=ΔBMC
=>AE=BC
ΔANF=ΔCNB
=>\(\widehat{NAF}=\widehat{NCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
ΔANF=ΔCNB
=>AF=CB
Ta có: AF=CB
AE=BC
Do đó: AE=AF
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
mà AE=AF
nên A là trung điểm của EF

1.
Xét tam giác AMB và tam giác NMC có:
AM = NM (gt)
AMB = NMC (2 góc đối đỉnh)
MB = MC (M là trung điểm của BC)
=> Tam giác AMB = Tam giác NMC (c.g.c)
Xét tam giác AMC và tam giác NMB có:
AM = NM (gt)
AMC = NMB (2 góc đối đỉnh)
MC = MB (M là trung điểm của BC)
=> Tam giác AMC = Tam giác NMB (c.g.c)
2.
Xét tam giác AME và tam giác BMC có:
AM = BM (M là trung điểm của AB)
AME = BMC (2 góc đối đỉnh)
ME = MC (gt)
=> Tam giác AME = Tam giác BMC (c.g.c)
=> AEM = BCM (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AE // BC
Xét tam giác ANF và tam giác CNB có:
AN = CN (N là trung điểm của AC)
ANF = CNB (2 góc đối đỉnh)
NF = NB (gt)
=> Tam giác ANF = Tam giác CNB (c.g.c)
=> AF = CB (2 cạnh tương ứng)

a: BC=căn 4^2+3^2=5cm
b: Xét ΔABC vuông tại A và ΔANM vuông tại A có
AB=AN
AC=AM
=>ΔABC=ΔANM
=>BC=NM
c: ΔANB vuông tại A có BA=AN
nên ΔANB vuông cân tại A
=>góc ANB=45 độ
ΔACM vuông tại A có AC=AM
nên ΔACM vuông cân tại A
=>góc ACM=45 độ=góc ANB
=>CM//NB

a) Vì M1 và M2 là 2 góc đối đỉnh
=>M1 = M2
hay tam giác AMD = tam giác BMC
(Mình ko làm được xin lỗi bạn nha)
( HÌNH vẽ hơi xấu )
CM
a) Xét tam giác MAI và tam giác MBC có:
\(\hept{\begin{cases}MA=MB\left(gt\right)\\\widehat{M1}=\widehat{M2}\left(2gocdoidinh\right)\\MI=MC\left(gt\right)\end{cases}\Rightarrow\Delta}MAI=\Delta MBC\left(c-g-c\right)\)
b) Xét tam giác NAK và tam giác NCB có:
\(\hept{\begin{cases}NA=NC\left(gt\right)\\\widehat{N1}=\widehat{N2}\left(2gocdoidinh\right)\\NB=NK\left(gt\right)\end{cases}}\Rightarrow\Delta NAK=\Delta NCB\left(c-g-c\right)\)
c) Vì \(\Delta MAI=\Delta MBC\left(cmt\right)\)
\(\Rightarrow\widehat{A1}=\widehat{ABC}\)( 2 góc t..ứng )
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AI//BC\left(1\right)\)
Vì \(\Delta NAK=\Delta NCB\left(cmt\right)\)
\(\Rightarrow\widehat{A2}=\widehat{ACB}\)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AK//BC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow A,I,K\)thẳng hàng ( định lý Py-ta-go )
Bạn ơi mình nhầm nhé dòng cuối cùng là theo tiên đề Ơ-clit nha xin lỗi