Cho tam giác $A B C$. Gọi $M$ là trung điểm của $A B$ và $N$ là một điểm trên cạnh $A C$ sao cho $N A=2 N C$. Gọi $K$ là...

TT

Thầy Tùng Dương

VIP

28 tháng 3 2022 - olm

Cho tam giác $A B C$. Gọi $M$ là trung điểm của $A B$ và $N$ là một điểm trên cạnh $A C$ sao cho $N A=2 N C$. Gọi $K$ là trung điểm $M N$. Phân tích vectơ $\overrightarrow{A K}$ theo $\overrightarrow{A B}$ và $\overrightarrow{A C}$.

#Toán lớp 10

6

L

✎﹏l๏gคภlєє︵²ᵏ¹⁰

28 tháng 3 2022

Đúng(0)

TT

(Tuấn) T̶r̶ư̶ở̶n̶g̶ 💎₮Ɇ₳₥ ₱ⱤØ🐬

28 tháng 3 2022

TL:

Đáp án:

$\text{KD = KA + AD = - AK + AD }$

$=-\frac{1}{2}\left(AM+AN\right)+\frac{1}{2}\left(AB+AC\right)$

$=-\frac{1}{2}\left(\frac{1}{2}AB+\frac{2}{3}AC\right)+\frac{1}{2}AB+\frac{1}{2}AC$

$=\frac{1}{4}AB+\frac{1}{6}AC$

HT

Đúng(0)

GD

Giang Đặng Nguyễn thu

30 tháng 10 2016

Cho tam giác ABC đường trung tuyến AD. Gọi I là trung điểm AD, điểm K nằm trên cạnh AC sao cho $\overrightarrow{KC}=-2\overrightarrow{KA}$

a) Hãy phân tích vectơ BI, BK theo vectơ BA, BC

b) Chứng minh B,I,K thẳng hàng

c) Nêu các xác định điểm M sao cho $27\overrightarrow{MA}-8\overrightarrow{MB}=2015\overrightarrow{MC}$

Nhanh nha gấp lắm

#Toán lớp 10

1

ND

Nguyễn Đức Thắng

8 tháng 11 2016

a)

$\overrightarrow{BI}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)$ (t/c trung điểm)

$=\frac{1}{2}\left(\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}\right)$

$=\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}$

$\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}$

$=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{AC}$

$=\overrightarrow{BA}+\frac{1}{3}\left(\overrightarrow{BC}-\overrightarrow{BA}\right)$

$=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}-\frac{1}{3}\overrightarrow{BA}$

$=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}$

b) Ta có: $\overrightarrow{BK}=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}=\frac{4}{3}\left(\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}\right)=\frac{4}{3}\overrightarrow{BI}$

=> B,K,I thẳng hàng

c) $27\overrightarrow{MA}-8\overrightarrow{MB}=2015\overrightarrow{MC}$

$\Leftrightarrow27\left(\overrightarrow{MC}+\overrightarrow{CA}\right)-8\left(\overrightarrow{MC}+\overrightarrow{CB}\right)=2015\overrightarrow{MC}$

$\Leftrightarrow27\overrightarrow{MC}+27\overrightarrow{CA}-8\overrightarrow{MC}-8\overrightarrow{CB}-2015\overrightarrow{MC}=\overrightarrow{0}$

$\Leftrightarrow-1996\overrightarrow{MC}+27\overrightarrow{CA}-8\overrightarrow{CB}=\overrightarrow{0}$

$\Leftrightarrow1996\overrightarrow{CM}=8\overrightarrow{CB}-27\overrightarrow{CA}$

$\Leftrightarrow\overrightarrow{CM}=\frac{8\overrightarrow{CB}-27\overrightarrow{CA}}{1996}$

Vậy: Dựng điểm M sao cho $\overrightarrow{CM}=\frac{8\overrightarrow{CB}-27\overrightarrow{CA}}{1996}$

Đúng(0)

SG

Sách Giáo Khoa

8 tháng 4 2017

Cho tam giác ABC. Gọi M là trung điểm của AB và N là một điểm trên canh AC sao cho NA = 2NC. Gọi K là trung điểm của MN

Phân tích vectơ $\overrightarrow{AK}$ theo $\overrightarrow{AB}$ và $\overrightarrow{AC}$ ?

#Toán lớp 10

1

BT

Bùi Thị Vân

15 tháng 5 2017

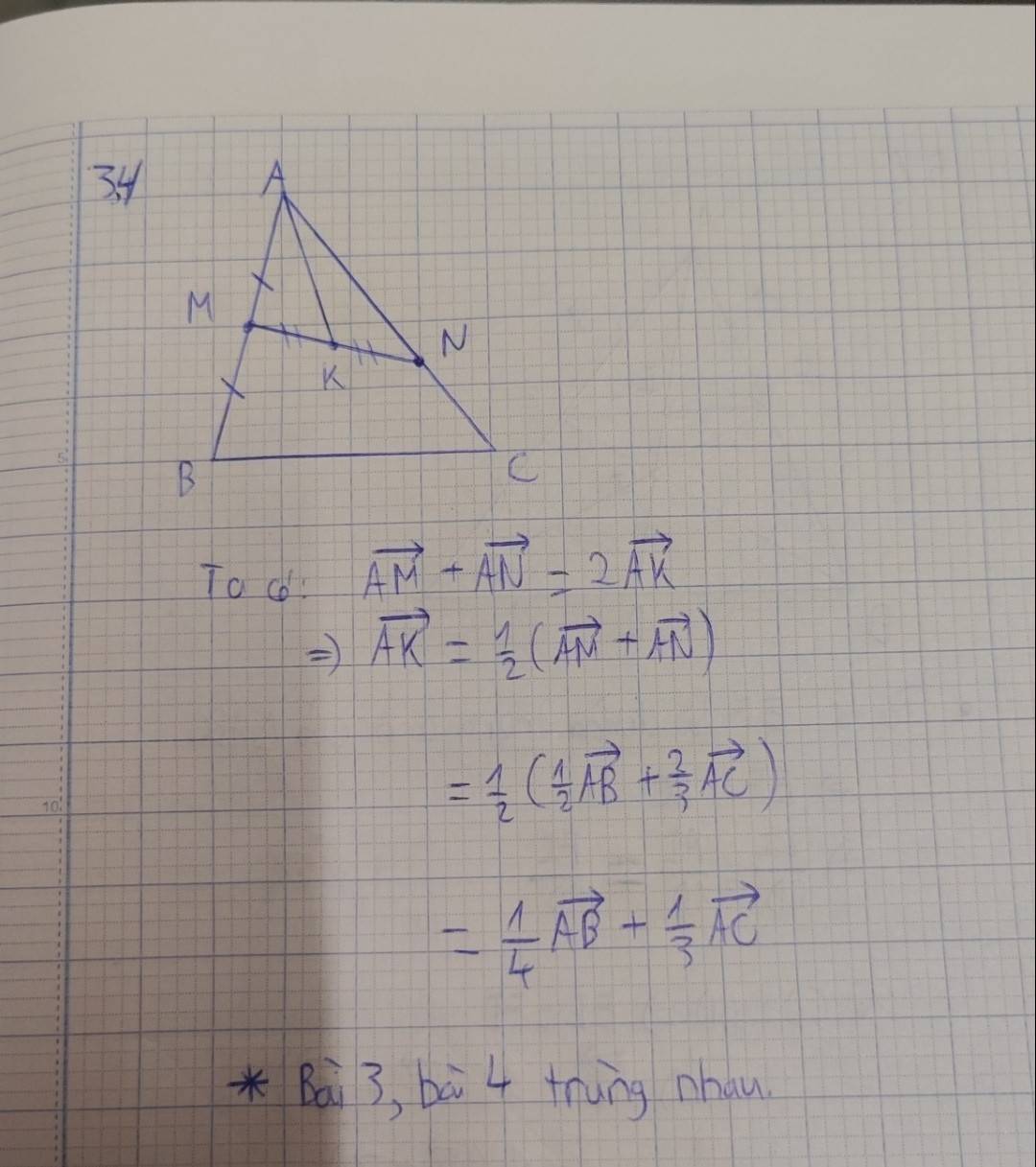
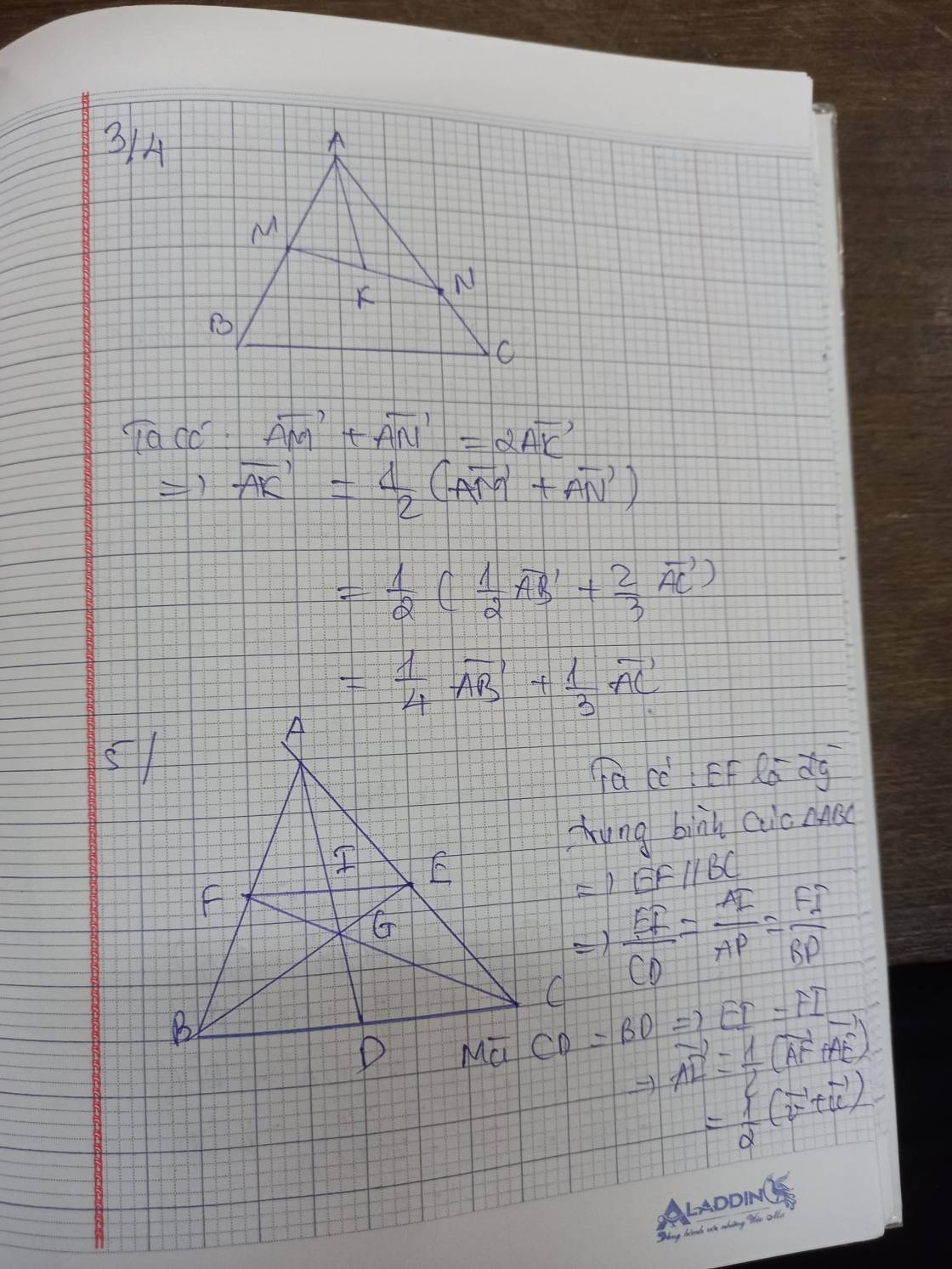
Theo các xác định điểm M, N ta có:
$\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB};\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}.$
Theo tính chất trung điểm của MN ta có:
$\overrightarrow{AK}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)$
$=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}$.

Đúng(0)

TT

Thầy Tùng Dương

VIP

28 tháng 3 2022 - olm

Cho tam giác $A B C$ có trung tuyên $A M$. Gọi $I$ là trung điếm của $A M$ và $K$ là điếm trên cạnh $A C$ sao cho $A K=\dfrac{1}{3} A C$. Chứng minh rằng ba điểm $B, I, K$ thẳng hàng. Ta có $\overrightarrow{B I}=\dfrac{1}{2}(\overrightarrow{B A}+\overrightarrow{B M})=\dfrac{1}{2}\left(\overrightarrow{B A}+\dfrac{1}{2} \overrightarrow{B C}\right)$

#Toán lớp 10

0

TT

Thầy Tùng Dương

VIP

28 tháng 3 2022 - olm

Cho tam giác $A B C$ có trọng tâm $G$. Cho các điểm $D, E, F$ lần lượt là trung điểm của $B C, C A$ $A B$ và $I$ là giao điểm của $A D$ và $E F$. Đạ̄t $\vec{u}=\overrightarrow{A E}, \vec{v}=\overrightarrow{A F}$. Hāy phân tích các vectơ $\overrightarrow{A I}, \overrightarrow{A G}, \overrightarrow{D E}$, $\overrightarrow{D C}$ theo hai vectơ $\vec{u}, \vec{v}$.

#Toán lớp 10

8

L

✎﹏l๏gคภlєє︵²ᵏ¹⁰

28 tháng 3 2022

undefined

#zinc

Đúng(0)

TQ

Trương Quốc Việt

20 tháng 11 2023

Đúng(0)

QN

Quỳnh Như

7 tháng 10 2021

cho tứ giác ABCD . gọi M,N lần lượt là trung điểm AB và CD .cmr: a) 2$\overrightarrow{mn}$=$\overrightarrow{AC}$+$\overrightarrow{BD}$=$\overrightarrow{BC}$+$\overrightarrow{AD}$b)Lấy H trên AD , K trên BC sao cho $\dfrac{HA}{HD}$=$\dfrac{KB}{KC}$. HK cắt MN tại I .cmr I là trung...

Đọc tiếp

#Toán lớp 10

0

K

Kuramajiva

11 tháng 10 2020

Cho tam giác ABC. Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho NA = 2NC. Gọi K là trung điểm của MN. Gọi D là trung điểm của BC. Hãy biểu diễn $\overrightarrow{KD}$ theo các vectơ $\overrightarrow{AB} $ và $\overrightarrow{AC}$

#Toán lớp 10

1

NV

Nguyễn Việt Lâm

Giáo viên

11 tháng 10 2020

$\overrightarrow{KD}=\overrightarrow{KA}+\overrightarrow{AD}=-\overrightarrow{AK}+\overrightarrow{AD}$

$=-\frac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)+\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)$

$=-\frac{1}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}\right)+\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$

$=\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$

Đúng(0)

CK

Cù Khắc Huy

31 tháng 10 2020 - olm

Cho tam giác ABC có trọng tâm G. M, N lần lượt là trung điểm của AB, BC. Lấy 2 điểm I, J sao cho $2\overrightarrow{IA}+3\overrightarrow{IC}=\overrightarrow{0}$, $2\overrightarrow{JA}+5\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{0}$a) CM: M, N, J thẳng hàng với J là trung điểm của BIb) Gọi E là điểm thuộc AB sao cho $\overrightarrow{AE}=k.\overrightarrow{AB}$. Xác định k sao cho C, E, J thẳng...

Đọc tiếp

#Toán lớp 10

0