Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có thể giải bài toán này bằng cách sử dụng công thức diện tích của hình bình hành, và áp dụng định lí hai đường cao trong tam giác để tính diện tích tam giác ABC.
Đầu tiên, ta cần tính diện tích tam giác ABC. Ta sẽ sử dụng định lí hai đường cao trong tam giác ABC để tính toán. Gọi H là hạt giác của góc A trong tam giác ABC, và gọi AH là đường cao kẻ từ A xuống BC. Ta sẽ sử dụng định lí hai đường cao trong tam giác ABC để tính diện tích của tam giác này:
$S_{ABC} = \frac{1}{2}AH \cdot BC$
Tiếp theo, ta cần tính diện tích của hình bình hành AEMK. Để làm điều này, ta sử dụng công thức diện tích của hình bình hành:
$S_{AEMK} = AE \cdot MK$
Ta có thể tính được AE và MK bằng cách sử dụng các hệ số tỉ lệ. Gọi x là độ dài BM, ta có:
$AE = \frac{AB}{BC} \cdot BM = \frac{S}{S_{ABC}} \cdot x$
$MK = \frac{MC}{BC} \cdot BM = \frac{S - SMCKS}{S_{ABC}} \cdot x$
Lưu ý rằng ta sử dụng diện tích của hình bình hành để tính các hệ số tỉ lệ này.
Cuối cùng, ta có thể tính diện tích của hình bình hành AEMK bằng cách thay các giá trị được tính toán vào công thức diện tích của hình bình hành:
$S_{AEMK} = AE \cdot MK = \frac{S}{S_{ABC}} \cdot x \cdot \frac{S - SMCKS}{S_{ABC}} \cdot x = \frac{S(S-SMCKS)}{S_{ABC}^2} \cdot x^2$
Vậy diện tích của hình bình hành AEMK là $\frac{S(S-SMCKS)}{S_{ABC}^2} \cdot x^2$.
Ta có Theo định lý talet MN//AC
\(\frac{AN}{AB}=\frac{CM}{BC}\left(1\right)\)
Theo định lý Talet MP//AB
\(\frac{AP}{AC}=\frac{BM}{BC}\left(2\right)\)
\(\left(1\right)+\left(2\right):\frac{AN}{AB}+\frac{AP}{AC}=\frac{CM}{BC}+\frac{MC}{BC}\)
\(\frac{CM}{BC}+\frac{MC}{BC}=1\)
\(\Rightarrow\frac{AN}{AB}+\frac{AP}{AC}=1\)
a: Xét tứ giác AEMF có
AE//MF
AF//ME
góc EAF=90 độ
Do đó: AEMF là hình chữ nhật
b: \(S_{ABC}=\dfrac{1}{2}\cdot6\cdot4=3\cdot4=12\left(cm^2\right)\)
Gọi giao điểm của NP với AB và AC lần lượt là I và J.
Gọi giao điểm của NM với BI là K; của MQ với JC là H.
Theo giả thiết ta suy ra K, H lần lượt là trung điểm của NM và MQ. Hơn nữa ta cũng có \(NM\perp BI;MQ\perp JC\)
Do NP // MQ mà \(MQ\perp JH\) nên \(NP\perp JH\)
\(\Rightarrow\widehat{AIJ}=90^o-\widehat{BAC}=30^o\)
Vậy nên \(\widehat{NIB}=\widehat{AIJ}=30^o\) (Hai góc đối đỉnh)
\(\Rightarrow\widehat{NIK}=90^o-\widehat{NIB}=60^o\)
Xét tứ giác NPQM có NP // MQ; NM // PQ nên NPQM là hình bình hành.
Vậy \(\widehat{PQM}=\widehat{INM}=60^o\)
Ta có \(\widehat{BMK}=90^o-\widehat{ABC}=30^o;\widehat{NMI}=\widehat{INM}=60^o;\widehat{CMH}=90^o-\widehat{ACB}=30^o\)
nên \(\widehat{IMH}=180^o-30^o-60^o-30^o=60^o\)
Suy ra \(\widehat{IMH}=\widehat{PQH}\left(=60^o\right)\)
Xét hình thang IPQM có \(\widehat{IMH}=\widehat{PQH}\) nên nó là hình thang cân.
Ta có H là trung điểm MQ, \(JH\perp MQ;JH\perp IP\) nên I là trung điểm IP.
Xét tam giác AIP có AJ là đường cao đồng thời trung tuyến nên AIP là tam giác cân tại A.
Vậy AJ cũng là phân giác hay \(\widehat{JAP}=\widehat{JAI}=60^o\)
Suy ra \(\widehat{JAP}=\widehat{ACB}\left(=60^o\right)\)
Mà chúng lại ở vị trí so le trong nên AP // BC.
a: Xét tứ giác AEMF có
AE//MF
ME//AF
Do đó: AEMF là hình bình hành
mà \(\widehat{FAE}=90^0\)
nên AEMF là hình chữ nhật
a: Xét tứ giác AEMF có
góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot4\cdot6=2\cdot6=12\left(cm^2\right)\)
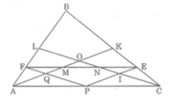
Gọi Q là giao điểm của PF và AK ,I là giao điểm của PE và CL
Trong △ FPE ta có: PE//AK hay QM //PE
Suy ra: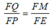 
(định lí ta-lét) (1)
Trong △ ALO ta có:PF //CL hay FQ //LO
Suy ra: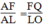
(định lí ta-lét) (2)
Trong △ ALC ta có: PF // CL
Suy ra: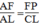 
(định lí ta-lét) (3)
Từ (2) và (3) suy ra: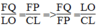 
Vì LO = 1/3 CL (O giao điểm của hai đường trung tuyến) nên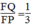 
(4)
Từ (1) và (4) suy ra: 
⇒ FM = 1/3 FE
Trong △ EPF ta có:PF // CL hay NI // PF
Suy ra: 
(định lí ta –lét) (5)
Trong △ CKO ta có: EI // OK
Suy ra: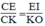 
(định lí ta –lét) (6)
Trong △ CKA ta có:PE // AK
Suy ra: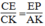 
(định lí ta –lét) (7)
Từ (6) và (7) suy ra: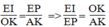 
Vì OK = 1/3 AK (O là giao điểm của hai đường trung tuyến) nên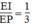 
(8)
Từ (5) và (8) suy ra: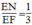 
⇒EN = 1/3 EF
Ta có: MN = EF - (EN + FM) = EF - (1/3 EF + 1/3 EF) = 1/3 EF
Vậy EN = MN = NF