Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B.
Đặt 
suy ra tập hợp các điểm M(z) = (x;y) là đường tròn (C) có tâm I(3;4) và bán kính R =
5
Ta có 
Ta cần tìm P sao cho đường thẳng ∆ và đường tròn (C) có điểm chung
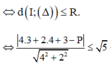
Do đó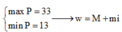 
Đáp án D.
Gọi z=x+yi ta có z-2-3i=x+yi-2-3i=x-2+(y-3)i.
Theo giả thiết 
nên điểm M biểu diễn cho số phức z nằm trên đường tròn tâm I(2;3) bán kính R=1.
Ta có
Gọi M(x;y) và H(-1;1) thì 
Do M chạy trên đường tròn, H cố định nên MH lớn nhất khi M là giao của HI với đường tròn.
Phương trình 
, giao HI và đường tròn ứng với t thỏa mãn:
nên 
Tính độ dài MH ta lấy kết quả HM= 13 + 1 .
Đáp án C
Đặt 
Số phức z được biểu diễn bởi điểm N(x;y)
Số phức 
được biểu diễn bởi điểm A(-2;1)
Số phức 
được biểu diễn bởi điểm B(5;-6)
được biểu diễn bởi điểm
Ta có: |z + 2 - i| + |z - 5 + 6i| = 7
2
Mà AB = 7
2
nên N thuộc đoạn thẳng AB.
Đường thẳng AB: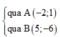 
=> phương trình đường thẳng AB là: x + y + 1 = 0
Vì N(x;y) thuộc đoạn thẳng AB nên x + y +1 = 0, x ∈ [-2;5]
Ta có: 
Xét 
trên [-2;5] ta có: f'(x) = 4(x-1)
Ta có:
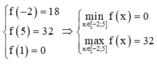
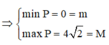
Vậy M + m = 4 2
Mọi điểm M biểu diễn z đều phải thỏa mãn 2 điều kiện: vừa thuộc đường tròn (C) vừa thuộc đường thẳng \(\Delta\) (tham số P)
Do đó, M là giao điểm của (C) và \(\Delta\)
Hay tham số P phải thỏa mãn sao cho (C) và \(\Delta\) có ít nhất 1 điểm chung
Hay hệ pt nói trên có nghiệm (thật ra chi tiết đó là thừa, chỉ cần biện luận (C) và \(\Delta\) có ít nhất 1 điểm chung \(\Rightarrow d\left(I;\Delta\right)\le R\) là đủ)
