Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

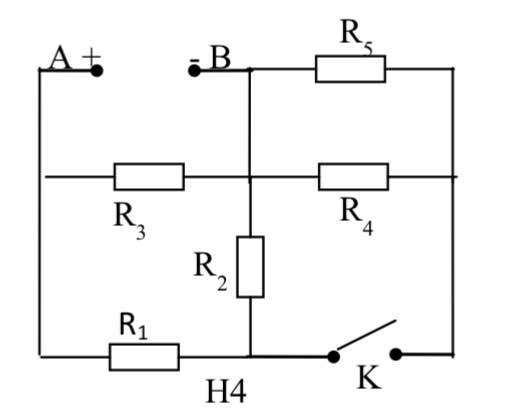
*Khi K mở \(=>\left(R1ntR3\right)//\left(R2ntR4\right)\)
\(=>I2=I4=I24=2A\)
\(=>Im=I1234=\dfrac{Uab}{Rtd}\)
\(=>Uab=I1234.Rtd\)
\(< =>12=\left(I13+I24\right).\dfrac{\left(R1+R3\right)\left(R2+R4\right)}{R1+R3+R2+R4}\)
\(< =>12=\left(\dfrac{12}{4+8}+2\right).\dfrac{\left(4+8\right)\left(2+R4\right)}{14+R4}=>R4=4\left(om\right)\)
** K đóng \(=>\dfrac{R1}{R3}=\dfrac{R2}{R4}\left(\dfrac{4}{8}=\dfrac{2}{4}\right)\)
\(=>I5=0A=>\left(R1ntR3\right)//\left(R2ntR4\right)\)
\(=>Uab=U13=U24=12V\)
\(=>I13=\dfrac{U13}{R13}=\dfrac{12}{R1+R3}=\dfrac{12}{4+8}=1A=I1=I3\)
\(=>I24=\dfrac{U24}{R24}=\dfrac{12}{2+4}=2A=I2=I4\)

â,\(=>Rtd=\dfrac{R1.R2}{R1+R2}=\dfrac{6.12}{6+12}=4\left(om\right)\)
b,\(=>U1=U2=12V=>I1=\dfrac{U1}{R1}=\dfrac{12}{6}=2A=>I2=\dfrac{U2}{R2}=1A\)
c, phải mắc \(\left(R1//R2\right)//R3\)
\(=>\)\(U3=12V\)
\(=>\dfrac{1}{Rtd}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=>\dfrac{1}{\dfrac{12}{3+0,5}}=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{R3}=>R3=24\left(om\right)\)
\(\)

a)Khóa K mở: \(R_1ntR_2\)
\(R_{12}=R_1+R_2=9+9=18\Omega\)
\(I=\dfrac{U}{R}=\dfrac{30}{18}=\dfrac{5}{3}A\)
b)Khóa K đóng: \(R_1nt\left(R_2//R_3\right)\)
\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{9\cdot18}{9+18}=6\Omega\)
\(R_{tđ}=R_1+R_{23}=9+6=15\Omega\)
\(I=\dfrac{U}{R}=\dfrac{30}{15}=2A\)

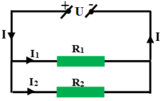
Vì R 3 song song với R 1 và R 2 nên:
U = U 1 = U 2 = U 3 = 4,8V
I = I 1 + I 2 + I 3 → I 3 = I - I 1 - I 2 = 1,5 – 0,8 – 0,4 = 0,3A
Điện trở
R
3
bằng: 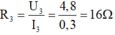
Điện trở tương đương của toàn mạch là: 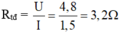

\(\Rightarrow\left\{{}\begin{matrix}R1ntR2\Rightarrow Rtd=R1+R2=\dfrac{U}{I}=\dfrac{16}{0,64}=25\left(\Omega\right)\left(1\right)\\R1//R2\Rightarrow Rtd=\dfrac{R1.R2}{R1+R2}=\dfrac{U'}{I'}=\dfrac{12}{2}=6\left(\Omega\right)\left(2\right)\\\end{matrix}\right.\)
\(\left(1\right)\left(2\right)\Rightarrow\left\{{}\begin{matrix}R1+R2=25\\\dfrac{R1R2}{R1+R2}=6\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}R2=25-R1\\\dfrac{R1\left(25-R1\right)}{R1+25-R1}=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}R2=25-R1\\-R1^2+25R1=150\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}R2=25-R1\\\left[{}\begin{matrix}R1=15\Omega\\R2=10\Omega\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}R1=15\Omega\\R2=25-15=10\Omega\end{matrix}\right.\\\left\{{}\begin{matrix}R1=10\Omega\\R2=15\Omega\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left(R1;R2\right)=\left\{\left(10;15\right);\left(15:10\right)\right\}\)
 Cho sơ đồ mạch điện như hình. Biết hđt ở 2 đầu AB là 12V không đổi. Khi K mở thì cường độ dòng điện qua mạch là 2A, khi K đóng thì cường độ dòng điện qua mạch tăng 0,5A. Tính điện trở R1 và R2 ?
Cho sơ đồ mạch điện như hình. Biết hđt ở 2 đầu AB là 12V không đổi. Khi K mở thì cường độ dòng điện qua mạch là 2A, khi K đóng thì cường độ dòng điện qua mạch tăng 0,5A. Tính điện trở R1 và R2 ?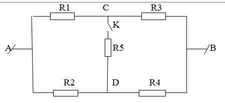
 không đổi; điện trở của dây dẫn và khoá không đáng kể.
không đổi; điện trở của dây dẫn và khoá không đáng kể.