NH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NG
1
H9
HT.Phong (9A5)
CTVHS
17 tháng 10 2023
a) \(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{19}+2^{20}\right)\)
\(A=2\cdot\left(1+3\right)+2^3\cdot\left(1+3\right)+...+2^{59}\cdot\left(1+3\right)\)
\(A=3\cdot\left(2+2^3+...+2^{59}\right)\)
Vậy A chia hết cho 3
________
\(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^3\right)+\left(2^2+2^4\right)+...+\left(2^{58}+2^{60}\right)\)
\(A=2\cdot\left(1+4\right)+2^2\cdot\left(1+4\right)+...+2^{58}\cdot\left(1+4\right)\)
\(A=5\cdot\left(2+2^2+...+2^{58}\right)\)
Vậy A chia hết cho 5
CM
7 tháng 7 2019
a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:
10 tháng 10 2021
4₁ A= 2 +2²³ +2 ² + + 220
a₁ A = 2₁ [1 + 2 +2²¹ +. +2¹2):2 Vay A chia hết choi
b₁ A = 2 + 2² +2²+ + 220 (2 +2²) + (2 ² + 2 9) + . + (219+220)
= 2₁ (1 + 2) + 2² (2+1). .. +2 19 (2+1) + = 2₁3 + 2³.3 + ..+ 219.3.
= (2+2 ³+ + 219) 3:3 Vậy A chia hết cho 3 A = 2 + 2 ² + 2³ + 2ª +. 20 + 2.9+ +2
2+2 ³ + 2² +2²4 + + 218 + 720 +2²³ +2²+ +218 +220 2. (2 +2²) + 2² (1+2²) +.. + 218 ( 1 +2²) = 2 5 +2²5 + + 218 5. 12 +2° + 2 ... +218 ) 5 : 5.
vậy A chia hết cho 5
DP
1
9 tháng 1 2023
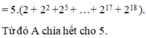
A=(1+2+2^2)+2^3(1+2+2^2)+...+2^96(1+2+2^2)+2^99
=7(1+2^3+...+2^96)+2^99 ko chia hết cho 7
AH
Akai Haruma
Giáo viên
25 tháng 2 2023
Lời giải:
$S=(2+2^2)+(2^3+2^4)+....+(2^{23}+2^{24})$
$=2(1+2)+2^3(1+2)+....+2^{23}(1+2)$
$=(1+2)(2+2^3+...+2^{23})$
$=3(2+2^3+...+2^{23})\vdots 3$
b.
$S=2+2^2+2^3+...+2^{23}+2^{24}$
$2S=2^2+2^3+2^4+....+2^{24}+2^{25}$
$\Rightarrow 2S-S=2^{25}-2$
$\Rightarrow S=2^{25}-2$
Ta có:
$2^{10}=1024=10k+4$
$\Rightarrow 2^{25}-2=2^5.2^{20}-2=32(10k+4)^2-2=32(100k^2+80k+16)-2$
$=10(320k^2+8k+51)\vdots 10$
$\Rightarrow S$ tận cùng là $0$
PT
1
CM
14 tháng 5 2019
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích sao cho tổng đó thành tích các thừa số trong đó có một thừa số chia hết cho 7. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: A = 2 + 2 2 + 2 3 + … + 2 60 = 2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + … + 2 58 + 2 59 + 2 60 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2 + 2 4 + … + 2 58 .7 ⇒ A ⋮ 7 |
PT
1
NB
0
13 tháng 1 2021
Bài 3:
a) Ta có: \(C=2+2^2+2^3+...+2^{99}+2^{100}\)
\(=\left(2+2^2+2^3+2^4+2^5\right)+\left(2^6+2^7+2^8+2^9+2^{10}\right)+...+\left(2^{96}+2^{97}+2^{98}+2^{99}+2^{100}\right)\)
\(=2\left(1+2+2^2+2^3+2^4\right)+2^6\left(1+2+2^2+2^3+2^4\right)+...+2^{96}\left(1+2+2^2+2^3+2^4\right)\)
\(=31\cdot\left(2+2^6+...+2^{96}\right)⋮31\)(đpcm)
13 tháng 1 2021
Bài 1:
Ta có: \(A=3^{n+2}-2^{n+2}+3^n-2^n\)
\(=3^n\cdot9-2^n\cdot4+3^n-2^n\)
\(=3^n\left(9+1\right)-2^n\left(4+1\right)\)
\(=10\left(3^n-2^{n-1}\right)⋮10\)
Vậy: A có chữ số tận cùng là 0
Bài 2:
Ta có: \(abcd=1000\cdot a+100\cdot b+10\cdot c+d\)
\(\Leftrightarrow abcd=1000\cdot a+96\cdot b+8c+2c+4b+d\)
\(\Leftrightarrow abcd=8\left(125a+12b+c\right)+\left(2c+4b+d\right)\)
mà \(8\left(125a+12b+c\right)⋮8\)
và \(2c+4b+d⋮8\)
nên \(abcd⋮8\)(đpcm)