Question

[Đào Phương Linh]

cho S=2.1+2.3+2.3²+..........+2.3²⁰⁰⁴

a)thu gọn S

b)tìm chữ số tận cùng của S. từ đó suy ra S không phải là số chính phương

Answer 1

[Mới vô]

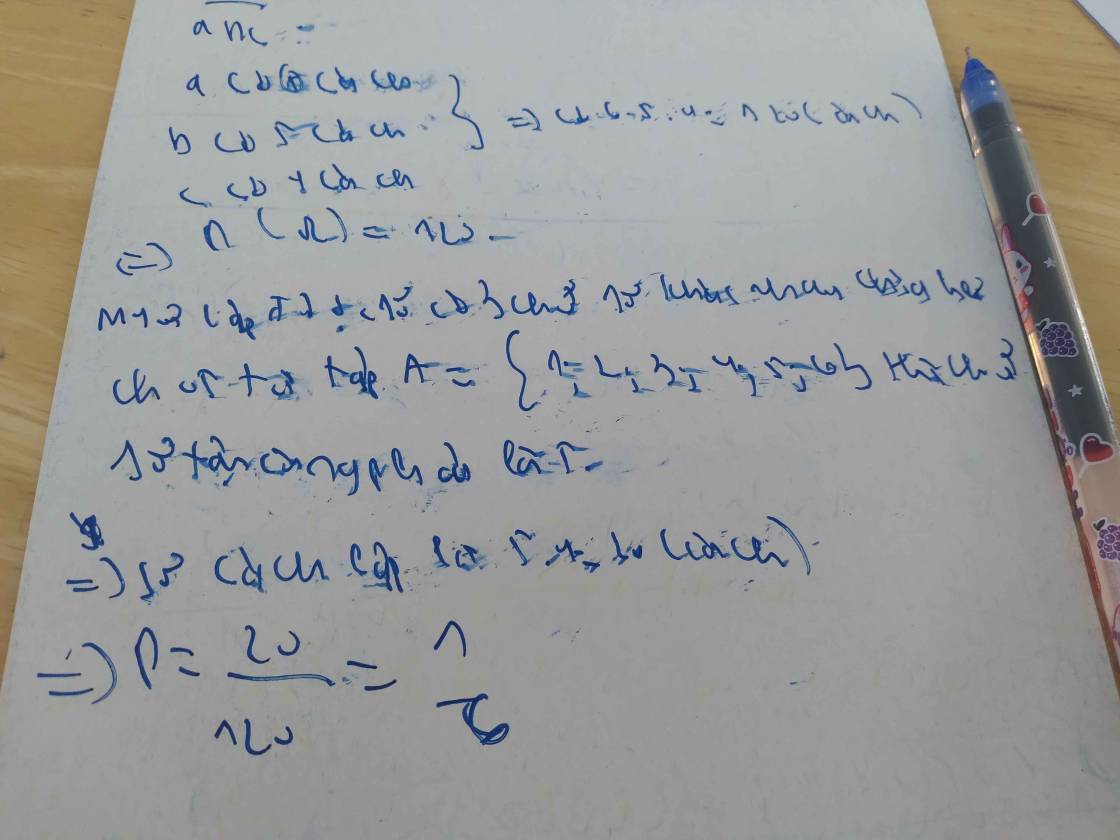
\(S=2\cdot1+2\cdot3+2\cdot3^2+...+2\cdot3^{2004}\\ =2\left(1+3+3^2+...+3^{2004}\right)\\ =3\left(1+3+3^2+...+3^{2004}\right)-\left(1+3+3^2+...+3^{2004}\right)\\ =\left(3+3^2+3^3+...+3^{2005}\right)-\left(1+3+3^2+...+3^{2004}\right)\\ =3^{2005}-1\)

\(3\equiv3\left(\text{mod }10\right)\\ 3^4\equiv1\left(\text{mod }10\right)\\3^{2004}= 3^{4^{501}}\equiv1^{501}\equiv1\left(\text{mod }10\right)\\ 3^{2005}=3\cdot3^{2004}\equiv3\cdot1\equiv3\left(\text{mod }10\right)\\ 3^{2005}-1\equiv3-1\equiv2\left(\text{mod }10\right)\)

Vì S tận cùng là 2 nên nó k phải là số chính phương