Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) thay m=1 vvào rồi giải như giải ptrinh bậc hai bình thường
b)chứng minh phương trrình (1) luôn có hai nghiệm phân biệt(tìm đenta, nếu đenta lớn hơn 0 thì pt có 2 nghiệm phân biệt)
Dựa vào hệ thức viet để giải một pt của hệ (thường thì là pt cộng)với pt đã cho ở đầu bài
thay lần lượt từng kết quả vào để tìm m
c)mk vẫn còn chưa thành thạo dạng này lắm nên chưa biết làm.

a) \(\Delta=4m^2-4\left(3m-4\right)=4m^2-12m+16=\left(2m-3\right)^2+7>0\)với mọi m=> pt (1) có nghiệm phân biệt với mọi m
b)áp dụng đ.lí Viét ta có: \(x_1+x_2=2m\); \(x_1.x_2=m^2+3m-4\)
\(x_1^2+x_2^2=\left(x1+x2\right)^2-2x1.x2=4m^2-2\left(m^2+3m-4\right)=4m^2-2m^2-6m+8\)
\(=2\left(m^2+3m-4\right)=2\left[\left(m+\frac{3}{2}\right)^2-4-\frac{9}{4}\right]=2\left[\left(m+\frac{3}{2}\right)^2-\frac{25}{4}\right]\)
A đặt giá trị nhỏ nhất khi m = -3/2

Để phương trình có 2 nghiệm thì: \(\Delta^'\ge0\)
Hay:\(2^2-\left(2m-5\right)\ge0\)
\(\Leftrightarrow4-2m+5\ge0\)
\(\Leftrightarrow-2m\ge-9\)
\(\Leftrightarrow m\le\frac{9}{2}\)
Theo Vi-ét, ta có: \(\hept{\begin{cases}x_1+x_2=-4\\x_1x_2=2m-5\end{cases}}\)
Ta có: \(x_1^2+x_2^2-x_1x_2=20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2=20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=20\)
\(\Leftrightarrow\left(-4\right)^2-3\left(2m-5\right)=20\)
\(\Leftrightarrow16-6m+15=20\)
\(\Leftrightarrow-6m=-11\)
\(\Leftrightarrow m=\frac{11}{6}\)(tm)
=.= hk tốt!!
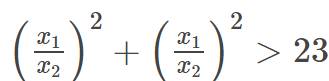

 Cho phương trình x2-(2m-1)x+4=0 (1)
Cho phương trình x2-(2m-1)x+4=0 (1)
Lời giải:
Để pt có 2 nghiệm $x_1,x_2$ thì: $\Delta=k^2-8\geq 0$
$\Leftrightarrow k^2\geq 8(1)$
Áp dụng định lý Viet:
$x_1+x_2=-k$
$x_1x_2=2$
Khi đó:
$(\frac{x_1}{x_2})^2+(\frac{x_2}{x_1})^2> 23$
$\Leftrightarrow \frac{x_1^4+x_2^4}{(x_1x_2)^2}>23$
$\Leftrightarrow x_1^4+x_2^4> 23(x_1x_2)^2=23.2^2=92$
$\Leftrightarrow (x_1^2+x_2^2)^2-2(x_1x_2)^2> 92$
$\Leftrightarrow (x_1^2+x_2^2)^2-8> 92$
$\Leftrightarrow [(x_1+x_2)^2-2x_1x_2]^2>100$
$\Leftrightarrow (k^2-4)^2>100$
$\Leftrightarrow k^2-4>10$ hoặc $k^2-4<-10$
$\Leftrightarrow k^2>14$ hoặc $k^2<-6$ (loại)
$\Leftrightarrow k> \sqrt{14}$ hoặc $k< -\sqrt{14}$
Kết hợp với $k^2\geq 8$ suy ra $k> \sqrt{14}$ hoặc $k< -\sqrt{14}$