Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để phương trình có 2 nghiệm
\(\Delta'\ge0\Rightarrow\left(-1\right)^2-1.3m\ge0\Leftrightarrow1-3m\ge0\Leftrightarrow1\ge3m\Leftrightarrow\dfrac{1}{3}\ge m\)
Theo hệ thức Vi-et ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-2\right)}{1}=2\\x_1x_2=\dfrac{3m}{1}=3m\end{matrix}\right.\)
Ta có:
\(x_1^2x_2^2=x_1+x_2+7\\ \Leftrightarrow x_1x_2.x_1x_2=x_1+x_2+7\\ \Rightarrow3m.3m=2+7\\ \Leftrightarrow9m^2-9=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1\left(tm\right)\\m=1\left(ktm\right)\end{matrix}\right.\)
Vậy m = -1

a)
\(m=6\)
\(\Rightarrow x^2+5x+6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\)
b)
\(\left|x_1-x_2\right|=3\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=9\)
\(\Leftrightarrow x_1^2=2x_1x_2+x^2_2=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=9\)
Mà \(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1-x_2=m\end{matrix}\right.\)
\(\Rightarrow25-4m=9\)
\(\Leftrightarrow4m=16\)
\(\Leftrightarrow m=4\)

\(x^2-2\left(m+4\right)x+m^2+8m-9=0\left(1\right)\)
Ta giải \(\Delta=[-2\left(m+4\right)]^2-4\left(m^2+8m-9\right)=100>0\forall m\)
suy ra pt có 2 nghiệm phân biệt \(x_1,x_2\forall m\).
Ta có: \(x_1=m-1\), \(x_2=m+1\) (thay \(\Delta\) vào công thức tìm nghiệm phân biệt).
Gọi \(A=\dfrac{x_1^2+x_2^2-48}{x_1^2+x_2^2}\).
\(\Rightarrow A=1-\dfrac{48}{x_1^2+x_2^2}=1-\dfrac{48}{\left(m-1\right)^2+\left(m+1\right)^2}=1-\dfrac{24}{m^2+1}\).
Để biểu thức A nguyên thì \(\dfrac{24}{m^2+1}\) nguyên, suy ra \(m^2+1\inƯ\left(24\right)\).
\(\Rightarrow m^2+1\in\left\{1;2;4;6;8;12;24\right\}\)
\(\Rightarrow m\in\left\{0;\pm1\right\}\) (vì m nhận giá trị nguyên)
Vậy \(m\in\left\{0;\pm1\right\}\) là giá trị cần tìm.
Mình chỉnh sửa lại một chút nhé.
\(A=1-\dfrac{24}{m^2+2}\)
\(\Rightarrow...\)\(\Rightarrow\)\(m^2+2\in\left\{1;2;3;4;6;8;12;24\right\}\)
\(\Rightarrow m\in\left\{0;\pm1;\pm2\right\}\)
Vậy...

a. thay m=-4 vào (1) ta có:
\(x^2-5x-6=0\)
Δ=b\(^2\)-4ac= (-5)\(^2\) - 4.1.(-6)= 25 + 24= 49 > 0
\(\sqrt{\Delta}=\sqrt{49}=7\)
x\(_1\)=\(\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+7}{2}\)=6
x\(_2\)=\(\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{5-7}{2}\)=-1
vậy khi x=-4 thì pt đã cho có 2 nghiệm x\(_1\)=6; x\(_2\)=-1

a, - Thay m = 6 vào phương trình ta được : \(x^2-5x+6=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
Vậy ...
b, - Xét phương trình trên có : \(\Delta=b^2-4ac=25-4m\)
- Để phương trình có 2 nghiệm phân biệt <=> \(m< \dfrac{25}{4}\)
- Theo viet ta có : \(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m\end{matrix}\right.\)
- Ta có : \(\left|x_1-x_2\right|=3\)
\(\Leftrightarrow x^2_1+x^2_2-2\left|x_1x_2\right|=\left(x_1+x_2\right)^2-2\left(x_1x_2+\left|x_1x_2\right|\right)=9\)
\(\Leftrightarrow m+\left|m\right|=8\)
\(\Leftrightarrow2m=8\)
\(\Leftrightarrow m=4\)
Vậy ...

a, với =-3
\(=>x^2-6x+6=0\)
\(\Delta=\left(-6\right)^2-4.6=12>0\)
=>pt có 2 nghiệm phân biệt x3,x4
\(=>\left[{}\begin{matrix}x3=\dfrac{6+\sqrt{12}}{2}=3+\sqrt{3}\\x4=\dfrac{6-\sqrt{12}}{2}=3-\sqrt{3}\end{matrix}\right.\)
b, \(\Delta=\left(2m\right)^2-4\left(m^2+m\right)=4m^2-4m^2-4m=-4m\)
pt đã cho đề bài có 2 nghiệm phân biệt x1,x2 khi
\(-4m>0< =>m< 0\)
theo vi ét \(=>\left\{{}\begin{matrix}x1+x2=-2m\\x1x2=m^2+m\end{matrix}\right.\)
có \(\left(x1-x2\right)\left(x1^2-x2^2\right)=32\)
\(< =>\left(x1-x2\right)^2\left(x1+x2\right)=32\)
\(< =>\left[x1^2-2x1x2+x2^2\right]\left(-2m\right)=32\)
\(< =>\left[\left(x1+x2\right)^2-4x1x2\right]\left(-2m\right)=32\)
\(< =>\left[\left(-2m\right)^2-4\left(m^2+m\right)\right]\left(-2m\right)=32< =>m=2\)(loại)
Vậy \(m\in\varnothing\)
Lời giải:
a. Với $m=-3$ thì pt trở thành:
$x^2-6x+6=0\Leftrightarrow x=3\pm \sqrt{3}$
b. Để pt có 2 nghiệm thì: $\Delta'=m^2-(m^2+m)=-m\geq 0$
$\Leftrightarrow m\leq 0$
Áp dụng định lý Viet: $x_1+x_2=-2m; x_1x_2=m^2+m$
Khi đó:
$(x_1-x_2)(x_1^2-x_2^2)=32$
$\Leftrightarrow (x_1-x_2)^2(x_1+x_2)=32$
$\Leftrightarrow [(x_1+x_2)^2-4x_1x_2](x_1+x_2)=32$
$\Leftrightarrow [(-2m)^2-4(m^2+m)](-2m)=32$
$\Leftrightarrow 8m^2=32$
$\Leftrightarrow m^2=4$
$\Rightarrow m=-2$ (do $m\leq 0$)
Vây.........

b) phương trình có 2 nghiệm \(\Leftrightarrow\Delta'\ge0\)
\(\Leftrightarrow\left(m-1\right)^2-\left(m-1\right)\left(m+3\right)\ge0\)
\(\Leftrightarrow m^2-2m+1-m^2-3m+m+3\ge0\)
\(\Leftrightarrow-4m+4\ge0\)
\(\Leftrightarrow m\le1\)
Ta có: \(x_1^2+x_1x_2+x_2^2=1\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=1\)
Theo viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\left(m-1\right)\\x_1x_2=\dfrac{c}{a}=m+3\end{matrix}\right.\)
\(\Leftrightarrow\left[-2\left(m-1\right)^2\right]-2\left(m+3\right)=1\)
\(\Leftrightarrow4m^2-8m+4-2m-6-1=0\)
\(\Leftrightarrow4m^2-10m-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m_1=\dfrac{5+\sqrt{37}}{4}\left(ktm\right)\\m_2=\dfrac{5-\sqrt{37}}{4}\left(tm\right)\end{matrix}\right.\Rightarrow m=\dfrac{5-\sqrt{37}}{4}\)

\(\Delta'=\left[-\left(m+4\right)\right]^2-1\left(m^2-8\right)=m^2+8m+16-m^2+8=8m+24\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow8m+24\ge0\Leftrightarrow m\ge-3\)
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2m+8\\x_1x_2=m^2-8\end{matrix}\right.\)
\(A=x^2_1+x^2_2-x_1-x_2\\ =\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\\ =\left(2m+8\right)^2-2\left(m^2-8\right)-\left(2m+8\right)\\ =4m^2+32m+64-2m^2+16-2m-16\\ =2m^2+30m+64\)
Amin=\(-\dfrac{97}{2}\)\(\Leftrightarrow m=-\dfrac{15}{2}\)
\(B=x^2_1+x^2_2-x_1x_2\\ =\left(x_1+x_2\right)^2-3x_1x_2\\ =\left(2m+8\right)^2-3\left(m^2-8\right)\\ =4m^2+32m+64-3m^2+24\\ =m^2+32m+88\)
Bmin=-168\(\Leftrightarrow\)m=-16

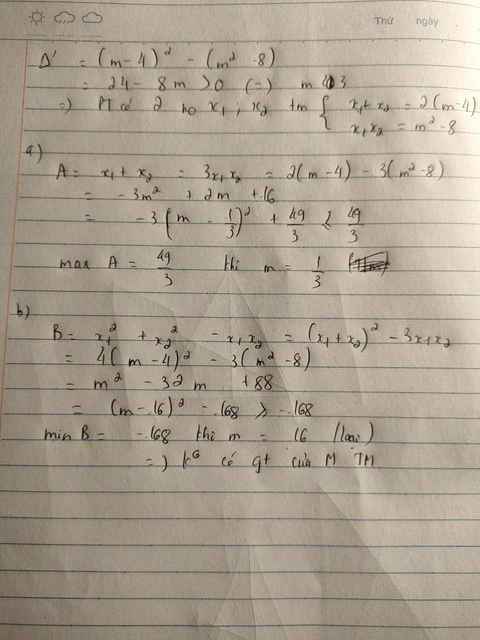
Ta có : \(x^2-5x+m=0\left(a=1;b=-5;c=m\right)\)
Theo hệ thức Vi et ta có : \(x_1+x_2=5;x_1x_2=m\)
Theo bài ra ta có : \(x_1^2+x_2^2+7=2\sqrt{x_2^2-3}+6x_1\)
Thay \(x_1;x_2\)lần lượt là \(x;y\)thì ta có phương trình mới :
\(x^2+y^2+7=2\sqrt{y^2-3}+6x\)
\(\Leftrightarrow\left(x+y\right)^2-2xy+7=2\sqrt{y^2-3}+6x\)
\(\Leftrightarrow\left(x+y\right)^2-2xy+7=2\sqrt{y^2-\sqrt{3}^2}+6x\)
\(\Leftrightarrow\left(x+y\right)^2-2xy+7=2\sqrt{y-\sqrt{3}}^2+6x\)
\(\Leftrightarrow\left(x+y\right)^2-2xy+7=2y-2\sqrt{3}+6x\)
\(\Leftrightarrow\left(x+y\right)^2-2xy+7=2\left(y-\sqrt{3}+3x\right)\)
\(\Leftrightarrow\frac{\left(x+y\right)^2-2xy+7}{2}=y-\sqrt{3}+3x\)
Mời idol về giải chứ chưa đi sâu vào mấy cái căn này lắm, phá mãi mới ra mà chả biết nhóm vào đâu.