Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp giải: Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
Lời giải:
Diện tích S của hình phẳng D được tính theo công thức là S = ∫ a b f x − g x d x

Gọi I1, I2, R1, R2 lần lượt là tâm và bán kính của các mặt cầu (S1) và (S2). Theo điều kiện tiếp xúc có I 1 A = R 1 ; I 2 B = R 2 .
Mặt khác hai mặt cầu tiếp xúc ngoài với nhau tại điểm M nên I 1 I 2 = R 1 + R 2 = I 1 A + I 2 B ⇒ I 1 I 2 luôn tiếp xúc với mặt cầu đường kính AB tại điểm M tức là M thuộc mặt cầu đường kính AB
Phương trình mặt cầu đường kính AB là ( S ) : x 2 + y - 1 2 + z - 2 2 = 9 có tâm I(0;1;2), R = 3.
Vì vậy M ∈ ( S ) ⇒ d M , P ≤ d I , P + R
=672+3=675.
Gọi 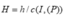
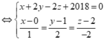
![]()
Dấu bằng đạt tại![]()
![]()
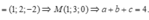
Chọn đáp án A.


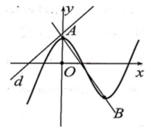

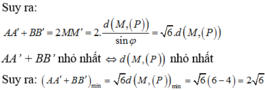







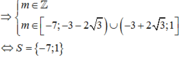

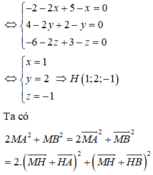

Chọn đáp án A
Giả sử A a ; a 2 và B b ; b 2 là hai điểm thuộc (P) và thỏa mãn AB = 2018.
Phương trình đường thẳng d đi qua hai điểm A và B là
Diện tích hình phẳng giới hạn bởi (P) và đường thẳng d là:
= 1 6 b - a 3
Gọi M là hình chiếu của A trên Ox và N là hình chiếu của B trên Ox. Suy ra M(a;0) và N(b;0).
Ta luôn có M N ≤ A B hay b - a = b - a ≤ 2018 .
Dấu “=” xảy ra khi MN//AB hay AB//Ox. Khi đó a = -1009; b = 1009.
Vậy S = 1 6 b - a 3 = 2018 3 6