Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.2:Sửa đề: (P): y=x^2
PTHĐGĐ là:
x^2-x-m=0
Δ=(-1)^2-4*1*(-m)=4m+1
Để (P) cắt (d) tại 1 điểm duy nhất thì 4m+1=0
=>m=-1/4

a) Vì (d) song song với đường thẳng \(y=-2x+2003\Rightarrow\left\{{}\begin{matrix}a=-2\\b\ne2003\end{matrix}\right.\)
\(\Rightarrow\left(d\right):y=-2x+b\)
Vì (d) cắt trục hoành tại điểm có hoành độ = 1
\(\Rightarrow\) tọa độ điểm đó là \(\left(1;0\right)\)
\(\Rightarrow1=b\Rightarrow\left(d\right):y=-2x+1\)
b) pt hoành độ giao điểm: \(-\dfrac{1}{2}x^2=-2x+2\Rightarrow\dfrac{1}{2}x^2-2x+2=0\)
\(\Rightarrow x^2-4x+4=0\Rightarrow\left(x-2\right)^2=0\Rightarrow x=2\Rightarrow y=-\dfrac{1}{2}.2^2=-2\)
\(\Rightarrow\) tọa độ giao điểm là \(\left(2;-2\right)\)

a) Ta có: đồ thị hàm số y=ax+b đi qua điểm A (2:1)
=> 2a+b=1 (1)
Lại có: đồ thị cắt trục tung tại điểm có tung độ bằng 5
=> b=5 (2)
Từ (1) và (2) ta có: 2a+5=1
=> a= -2
b) Gía trị của m để (P) và (d) có 1 điểm chung duy nhất là
3x2 =2x+m
=> 3x2-2x-m
\(\Delta'=1+3m\)
=> m= -1/3
Tọa độ điểm chung là:
3x2=2x-1/3
=> 3x2-2x+1/3
=> x=1/3
thay x=1/3 vào vào parabol (P) ta đc: y= 3(1/3)2
y=1/3
=> Tọa độ ddiemr chung là (1/3; 1/3)

b: Phương trình hoành độ giao điểm là:
\(x^2+2x-b=0\)
Δ=4+4b
Để (P) tiếp xúc với (D) thì 4b+4=0
hay b=-1

`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
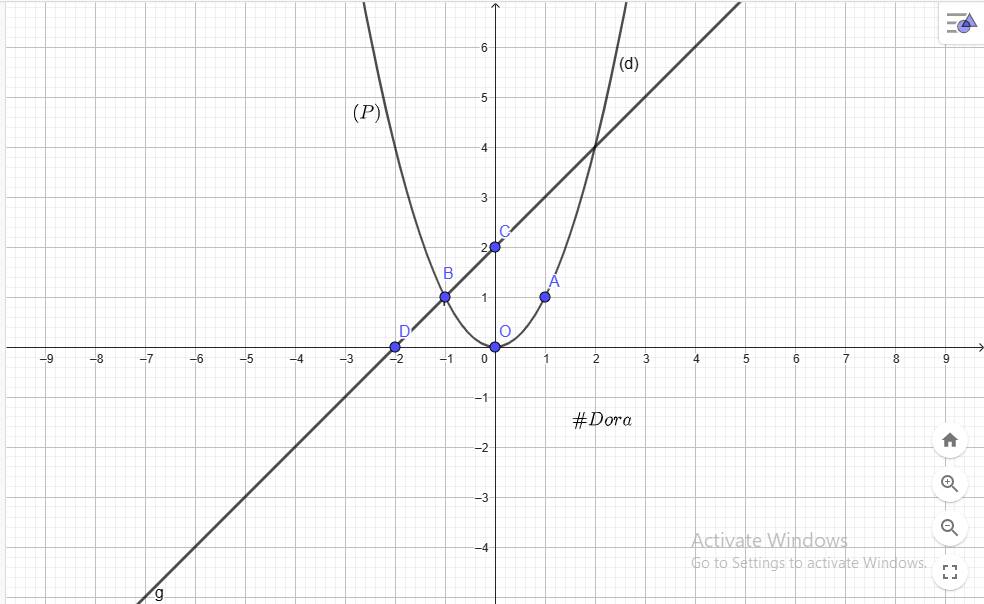
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`

a:
b: PTHĐGĐ là:
2x^2-(2m-2)x+m-1=0
Δ=(2m-2)^2-4*2*(m-1)
=4m^2-8m+4-8m+8
=4m^2-16m+12
=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)
Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0
=>m>3 hoặc m<1