Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

â) Xét tứ giác PAOB , co :
\(\widehat{A}=90^o\) ( PA là tiếp tuyến )
\(\widehat{B}=90^o\)( PB là tiếp tuyến )
\(\widehat{A}+\widehat{B}=90^o+90^o=180^o\)
Vay : tứ giác PAOB nội tiếp ( vì có tổng số đo hai góc đối diện bằng 180o )
b) Xét \(\Delta PAEva\Delta PCA,co:\)
\(\widehat{P}\) là góc chung
\(\widehat{ACE}=\widehat{EAP}\) ( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung )
Do đó : \(\Delta PAE~\Delta PCA\)( g - g )
\(=>\frac{PA}{PE}=\frac{PC}{PA}\)
\(=>PA^2=PE.PC\)
c)
c, ta có góc APC=PCB (slt vì BC//PA)
mà góc PCB=PBE =1/2sđcungBE ( góc nội tiếp chắn cung BE và góc tạo bởi tia tiếp tuyến và dây cung BE)
suy ra góc APC=PBE
xét hai tam giác PIE và BIP có
góc I chung
góc IBE=IBP(cmt)
suy ra hai tam giác đó đồng dạng
suy ra PI/BI=IE/PI
suy ra PI^2=BI*IE (1)
xét hai tam giác AIE và BIA có
góc I chung
góc IAE=ABI=1/2sđ cung AE ( góc nội tiếp chắn cung AE và góc tạo bởi tia tiếp tuyến và dây cung AE)
suy ra hai tam giác đó đồng dạng
suy ra AI/BI=EI/AI
suy ra AI^2=BI*EI (2)
từ 1 và 2 suy ra PI=AI( đpcm)

Xét ΔBAC và ΔBDA có
góc BAC=góc BDA
góc ABC chung
=>ΔBAC đồng dạng với ΔBDA
=>BA/BD=BC/BA
=>BA^2=BD*BC=PB^2
=>BP/BC=BD/BP
=>ΔBPD đồng dạng với ΔBCP
=>góc BPC=góc BDP
=>góc BPC=góc PEF
=>EF//AP

Xét ΔPAC và ΔPEA có
góc PAC=góc PEA
góc APC chung
=>ΔPAC đồng dạng với ΔPEA
=>PA/PE=PC/PA
=>PA^2=PE*PC=4*AB^2

a ) Ta có : PA // BC => ^MPE = ^ECB = ^PBM vì PB là tiếp tuyến của (O)
=> \(\Delta MPE~\Delta MBP\left(g.g\right)\)
\(\Rightarrow\frac{MP}{MB}=\frac{ME}{MP}\Rightarrow MP^2=ME.MB\)
b ) .Ta có MA là tiếp tuyến của (O)
\(\Rightarrow\widehat{MAE}=\widehat{MBA}\Rightarrow\Delta MAE~\Delta MBA\left(g.g\right)\)
\(\Rightarrow\frac{MA}{MB}=\frac{ME}{MA}\Rightarrow MA^2=ME.MB\)
\(\Rightarrow MA^2=MP^2\Rightarrow MA=MP\Rightarrow M\) là trung điểm PA

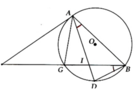
a, Chứng minh được P A 2 = P C . P B và P A 2 = P O 2 = O A 2 => tính được PO
b, Chứng minh được D B C ^ = D A B ^ = 1 2 C A B ^ => ĐPCM