HH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HA
1
4 tháng 4 2017
Bài giải:
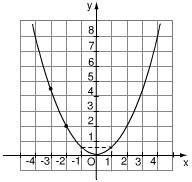
a) Theo hình vẽ, ta lấy điểm A thuộc đồ thị có tọa độ là x = -2, y = 2. Khi đó ta được:
2 = a . (-2)2 suy ra a = 
b) Đồ thị có hàm số là y = x2 . Tung độ của điểm thuộc parabol có hoành độ x = -3 là y = (-3)2 suy ra y = 
.
c) Các điểm thuộc parabol có tung độ là 8 là:
8 = x2 ⇔ x2 = 16 ⇔ x = ± 4
Ta được hai điểm và tọa độ của hai điểm đó là M(4; 8) và M'(-4; 8).
6 tháng 3 2022
b: f(-1)=-1
f(1/2)=-1/4
c: \(f\left(1\right)=-1^2=-1=y_E\)
Do đó: E thuộc đồ thị
\(f\left(-2\right)=-\left(-2\right)^2=-4< >y_F\)
Do đó: F không thuộc đồ thị
d: Thay x=-3 vào f(x), ta được:
\(f\left(-3\right)=-\left(-3\right)^2=-9\)
HH
2
10 tháng 5 2022
Điểm A có tung độ là 8 khi đó y =8
=> 2X^2 = 8
=> X^2 = 4
=> X1= 2, X2 = -2
Tọa độ của A có thể là (2;8) hoặc (-2;8)
12 tháng 5 2022
* Tung độ là 8 ⇒ y = 8
⇒ \(2x^2\) = 8
⇔ \(x^2\) = 4
⇔ \(\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Vậy tọa độ điểm A là ( 0 ; 2 ) và ( 0 ; -2 )
TH
4 tháng 3 2021
1) a đi qua A (1;-2) suy ra -2=1a hay a = -2 vậy đồ thị là y = -2x
2) 
3) điểm thuộc P có hoành độ = 2 suy ra x=2 hay y = -2*2=-4 vậy điểm đó là B(2;-4)
4) điểm thuộc P có tung độ bằng -4 suy ra -4 = -2x hay x=2 vậy điểm đó là C(2;-4)
4 tháng 3 2021
1) Để (P) đi qua điểm A(1;-2) thì
Thay x=1 và y=-2 vào hàm số \(y=ax^2\), ta được:
\(a\cdot1^2=-2\)
hay a=-2
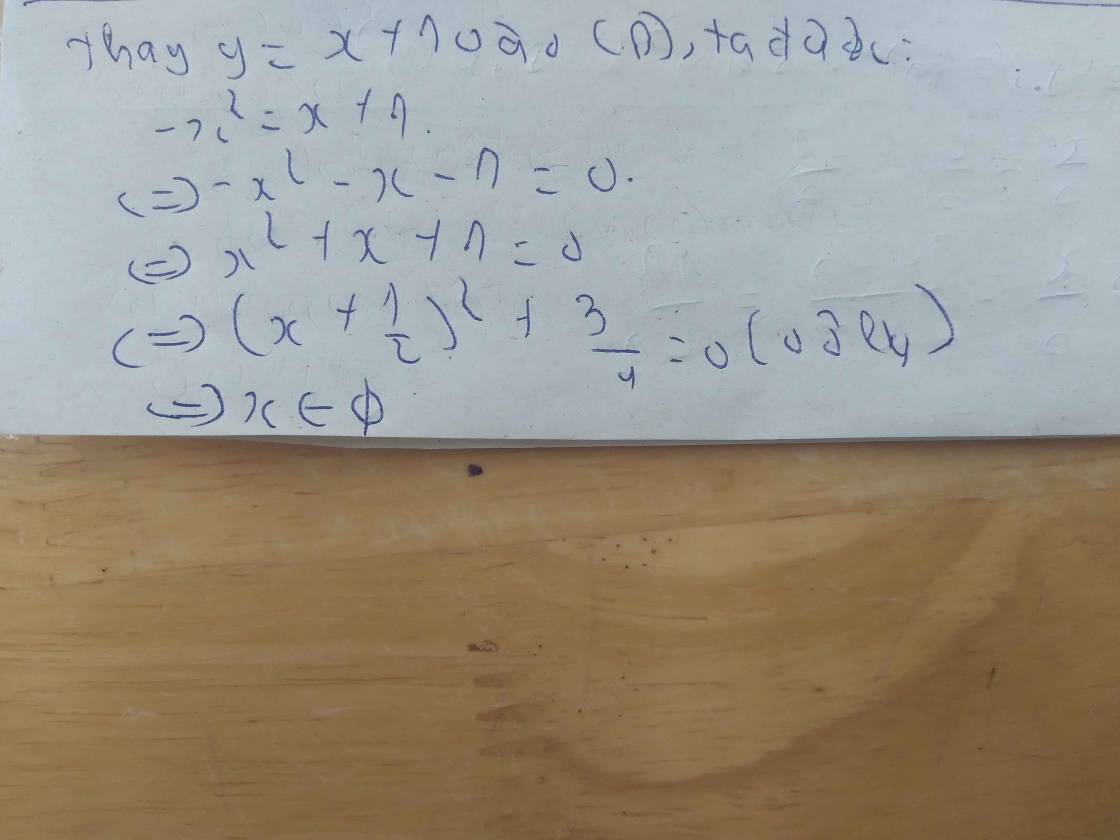
Thay x=-2 vào (P), ta được:
\(y=-2\cdot4=-8\)