


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





\(S_{OKN}=\dfrac{1}{2}\cdot OK\cdot KN< =\dfrac{1}{2}\cdot\dfrac{OK^2+ON^2}{2}=\dfrac{R^2}{4}\)
Dấu = xảy ra khi MO=MA

a, Ta co 2 bo de quen thuoc sau : FC la phan giac ^EFD, FB la phan giac PFD
ma QR//EP nen
\(\widehat{PFB}=\widehat{FQD}=\widehat{QFD}\Rightarrow\Delta DFQ\) can tai D => DF=DQ (1)
mat khac theo tinh chat tia phan giac ngoai ^PFD co \(\frac{FD}{FP}=\frac{CD}{CP}\)
ma \(\frac{CD}{CP}=\frac{DT}{PF}\) (DT//PF)
suy ra \(\frac{DF}{PF}=\frac{DT}{PF}\Rightarrow DT=DF\) (2)
Tu(1)va (2) suy ra DT=DQ hay D la trung diem QT
b, Goi S la trung diem BC ta chung minh PQSR noi tiep
Co \(\Delta PSE~\Delta ESD\left(G-G\right)\Rightarrow\frac{PS}{ES}=\frac{ES}{SD}\Leftrightarrow ES^2=PS.DS\)
lai co ES=SB=SC do S la trung diem canh huyen BC cua tam giac vuong BEC
suy ra \(BS^2=PS.SD=DS\left(PD+DS\right)=SD^2+PD.DS\)
=> \(PD.DS=BS^2-SD^2=\left(BS-DS\right)\left(BS+DS\right)=BD.DC\) (3)
Mat khac ^DQB=^PFB(cmt)
^PFB=^RCD( BFEC nt)
suy ra ^DQB=^RCD=> BQCR noi tiep
=> \(BD.DC=DQ.DR\) (4)
Tu (3),(4) suy ra DP.DS=DQ.DR => PQDR noi tiep
=> (PQR) di qua S la trung diem BC co dinh
c,lay H' doi xung voi H qua BC, ta co H' thuoc (O) .
ta lai co bo de sau : \(BD.DC=DH.DA\) (quen thuoc)
suy ra \(DP.DS=DH.DA\left(=DB.DC\right)\)
<=> \(\frac{DH}{DP}=\frac{DS}{DA}\)
ma ^HDP=^SDA=90
suy ra \(\Delta DHP~\Delta DSA\left(c-g-c\right)\Rightarrow\widehat{DHP}=\widehat{DSA}\)
va \(\widehat{DSA}=\widehat{AHK}\left(phu\widehat{DAS}\right)\)
=>\(\widehat{DHP}=\widehat{AHK}\) => P,H,K thang hang
lai co \(\widehat{AFH}=\widehat{AKH}=\widehat{AEH}=90\)
=> A,F,H,K,E cung thuoc 1 duong tron =. FHKE noi tiep
=>\(PF.PE=PH.PK\) (5)
ma BFEC noi tiep => \(PF.PE=PB.PC\) (6)
(5)+(6)Suy ra \(PH.PK=PB.PC\) => BHKC noi tiep
Vi H' ,I doi xung voi H,K qua BC ma BHKC noi tiep => BH'IC noi tiep
do vay \(I\in\left(BH'C\right)=\left(ABH'C\right)=\left(O\right)\)
e,Goi tam (CJL) la U, (U) cat (O) tai V, BC giao OG tai X
=> \(\widehat{VBG}=\widehat{VJG}\left(=\widehat{VCB}\right)\) =>BJVG noi tiep
=> B,J,X,V,G cung thuoc 1 duong tron => ^BVG=^BXG=90
lai co ^XVG +^XBG=180 hay ^XVG+^BAC=180
va ^BVC+^BAC=180
suy ra ^XVG=^BVC
hay 90 +^XVB=^XVB+^XVC
=> ^XVC=90
=> V thuoc duong tron dk XC
mat khac V cung thuoc (O)
suy ra V co dinh ,C co dinh
suy ra tam U di chuyen tren trung truc VC co dinh (dpcm)

a, b, c HS tự làm
d, Gợi ý: G' ÎOI mà I G ' I O = 1 3 => G' thuộc (G'; 1 3 R)

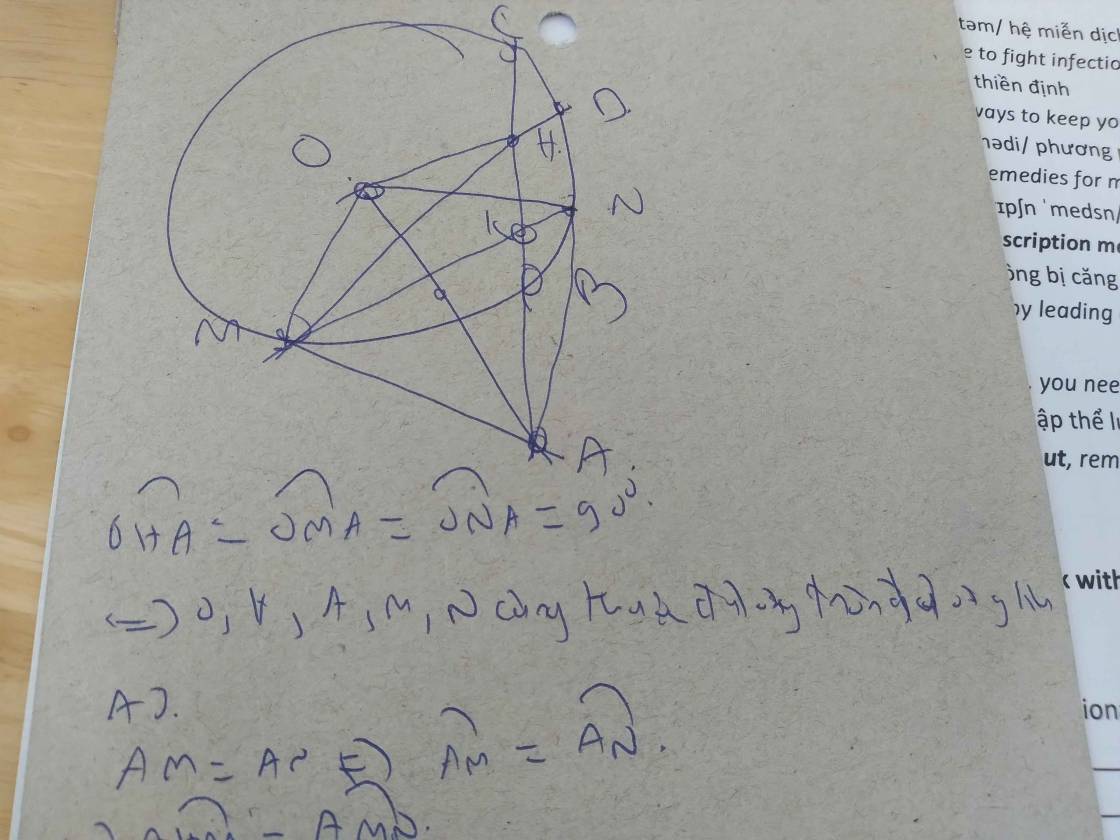
1) Trong (O) có BC là dây cung không đi qua O,có H là trung điểm BC
\(\Rightarrow OH\bot BC\Rightarrow\angle OHA=90\) mà \(\angle OMA=90\Rightarrow OMAH\) nội tiếp
2) Ta có: \(\Delta AMO\) vuông tại M có \(AO\bot MI\Rightarrow AM^2=AI.AO\)
1.
Theo giả thiết: \(H\) là trung điểm BC
\(\Rightarrow OH\perp BC\Leftrightarrow\widehat{OHA}=90^o\)
Lại có: \(AM\perp OM\Leftrightarrow\widehat{OMA}=90^o\)
\(\Rightarrow\widehat{OHA}+\widehat{OMA}=180^o\)
\(\Rightarrow AMOH\) nội tiếp
Hay \(A,M,O,H\) cùng thuộc đường tròn đường kính OA

Gọi S là trung điểm của đoạn OM, H là hình chiếu của S trên DE. Khi đó khoảng cách từ S đến DE là SH.
Ta sẽ chỉ ra SH = const, thật vậy: Do BM,CM là các tiếp tuyến tại B,C của (O) nên ^OBM = ^OCM (=900)
=> Tứ giác BOCM nội tiếp (OM). Ta cũng có: ^MEC = ^BAC (Vì ME // AB)
Theo tính chất góc tạo bởi tiếp tuyến và dây có ^BAC = ^MBC. Do đó ^MEC = ^MBC
=> Tứ giác MCEB nội tiếp. Tương tự, tứ giác MBDC nội tiếp
Từ đó sáu điểm B,D,O,E,C,M cùng thuộc đường tròn (OM) tâm là S => SD = SE = OM/2
Ta lại có OM2 = OC2 + CM2 = const (Vì O,C,M cố định) => SD = SE = const
Mặt khác ^DSE = 2^DME = 2^BAC = Sđ(BC = const => ^SDE = const => Sin^DSE = const
Hay \(\frac{SH}{SD}=const\). Mà SD không đổi nên SH không đổi => H cách S một khoảng không đổi
Ta thấy S cố định => (S;SH) cố định. Do DE vuông góc SH tại H nên DE luôn tiếp xúc với (S;SH) cố định (đpcm).

a: ΔOBC cân tại O
mà OH là trung tuyến
nên OH vuông góc BC
góc OHA+góc ONA=180 độ
=>OHAN nội tiếp
góc OMA+góc ONA=90+90=180 độ
=>OMAN nội tiếp
b: Xét ΔAMB và ΔACM có
góc AMB=góc ACM
góc BAM chung
=>ΔAMB đồng dạng với ΔACM
=>AM/AC=AB/AM
=>AM^2=AB*AC
bài đầy đủ đây bạn nhé
https://www.youtube.com/watch?v=DiI4Jz-LYQ4

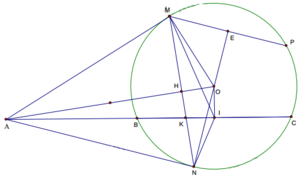
Ta có AN ⊥ NO, MP ⊥ NO, M ∉ AN => AN // MP
Do đó AMPN là hình bình hành ó AN = MP = 2x
Tam giác ∆ANO đồng dạng với ∆NEM => A N N E = N O E M = > N E = 2 x 2 R
TH 1.NE = NO – OE => 2 x 2 R = R − R 2 − x 2 ⇔ 2 x 2 = R 2 − R R 2 − x 2
Đặt R 2 − x 2 = t , t ≥ 0 ⇒ x 2 = R 2 − t 2 .
PTTT 2 ( R 2 − t 2 ) = R 2 − R t ⇔ 2 t 2 − R t − R 2 = 0 ⇔ 2 t = − R t = R
Do t ≥ 0 ⇒ t = R ⇔ R 2 − x 2 = R ⇔ x = 0 ⇒ A ≡ B (loại)
TH 2 NE = NO + OE => 2 x 2 R = R + R 2 − x 2 ⇔ 2 x 2 = R 2 + R R 2 − x 2
Đặt R 2 − x 2 = t , t ≥ 0 ⇒ x 2 = R 2 − t 2 .
PTTT 2 ( R 2 − t 2 ) = R 2 + R t ⇔ 2 t 2 + R t − R 2 = 0 ⇔ 2 t = R t = − R
Do t ≥ 0 ⇒ 2 t = R ⇔ 2 R 2 − x 2 = R ⇔ x = R 3 2 = > A O = 2 R (loại)
Vậy A thuộc BC, cách O một đoạn bằng 2R thì AMPN là hbh

1, Xét $(O)$ có các tiếp tuyến $AM;AN$
suy ra $\widehat{AMO}=\widehat{ANO}=90^o;AM=AN;AO$ là phân giác $\widehat{MAN}$
nên $\widehat{AMO}+\widehat{ANO}=180^o$
suy ra tứ giác $AMON$ nội tiếp (tổng 2 góc đối =180 độ)
2, Ta có: $AM=AN⇒ΔAMN$ cân tại $A$
có đường phân giác $AO$
$⇒AO$ đồng thời là đường trung trực tam giác $AMN$
$⇒AO⊥MN$ tại $H$
3. Xét $ΔAMO$ vuông tại $M$
$MH$ là đường cao
Nên $AH.AO=AM^2$ (hệ thức lượng trong tam giác vuông)
Xét $(O)$ có: Tiếp tuyến $AM$
nên $\widehat{AMB}=\widehat{MCB}$ (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung $BM$)
hay $\widehat{AMB}=\widehat{ACM}$
Xét tam giác $AMB$ và tam giác $ACM$ có:
$\widehat{AMB}=\widehat{ACM}$
$\widehat{A}$ chung
Nên tam giác $AMB$ và tam giác $ACM$ đồng dạng (g.g)
suy ra $\dfrac{AB}{AM}=\dfrac{AM}{AC}$
nên $AM^2=AB.AC$
Từ đó suy ra $AH.AO=AB.AC$