Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Vì MA,MB là tiếp tuyến của (O)
→ˆMAO=ˆMBO=90o→MAO^=MBO^=90o
→M,A,O,B→M,A,O,B thuộc đường tròn đường kình OM
b.Vì MA,MBMA,MB là tiếp tuyến của (O)→MO⊥AB=I→MO⊥AB=I
→OA2=OI.OM→OA2=OI.OM
C
Vì OF⊥CM=EOF⊥CM=E
→ˆFAC=ˆFEC=90o→◊AFCE,◊MAEO→FAC^=FEC^=90o→◊AFCE,◊MAEO nội tiếp
→M,A,E,O,B→M,A,E,O,B cùng thuộc một đường tròn
→ˆFCA=ˆFEA=ˆFBO→FCA^=FEA^=FBO^
→FC→FC là tiếp tuyến của (O)

Câu hỏi của Mafia - Toán lớp 9 - Học toán với OnlineMath
Em có thể tham khảo tại đây nhé.

a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó; MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
b: Ta có: ΔONC cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)NC tại I
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
Xét ΔOIM vuông tại I và ΔOHK vuông tại H có
\(\widehat{IOM}\) chung
Do đó: ΔOIM đồng dạng với ΔOHK
=>\(\dfrac{OI}{OH}=\dfrac{OM}{OK}\)
=>\(OI\cdot OK=OH\cdot OM=R^2\)
=>\(OI\cdot OK=OC\cdot OC\)
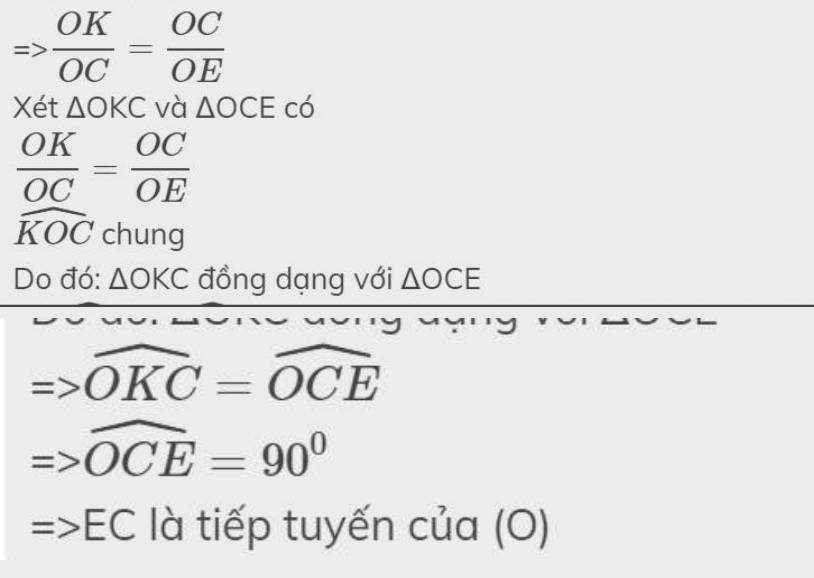
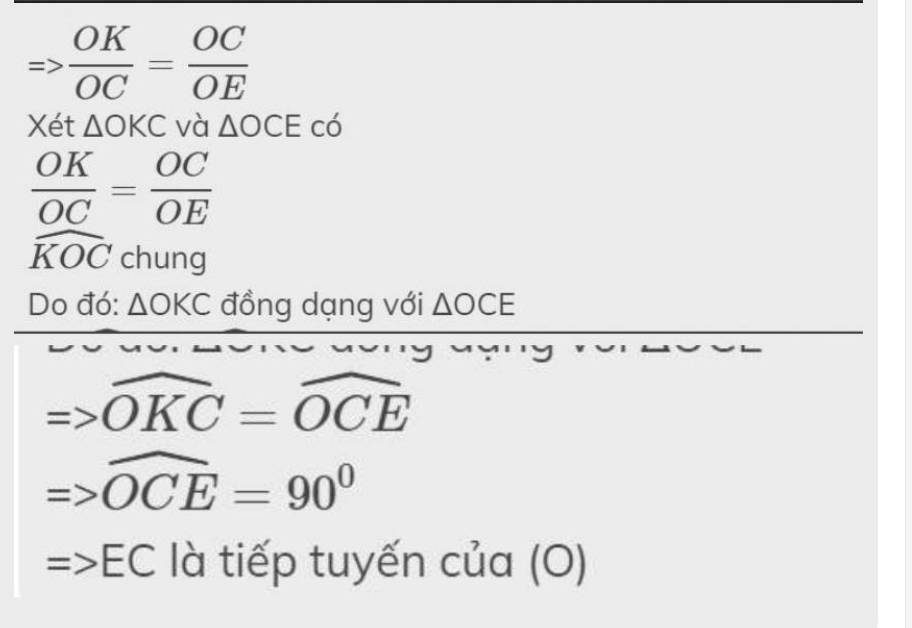
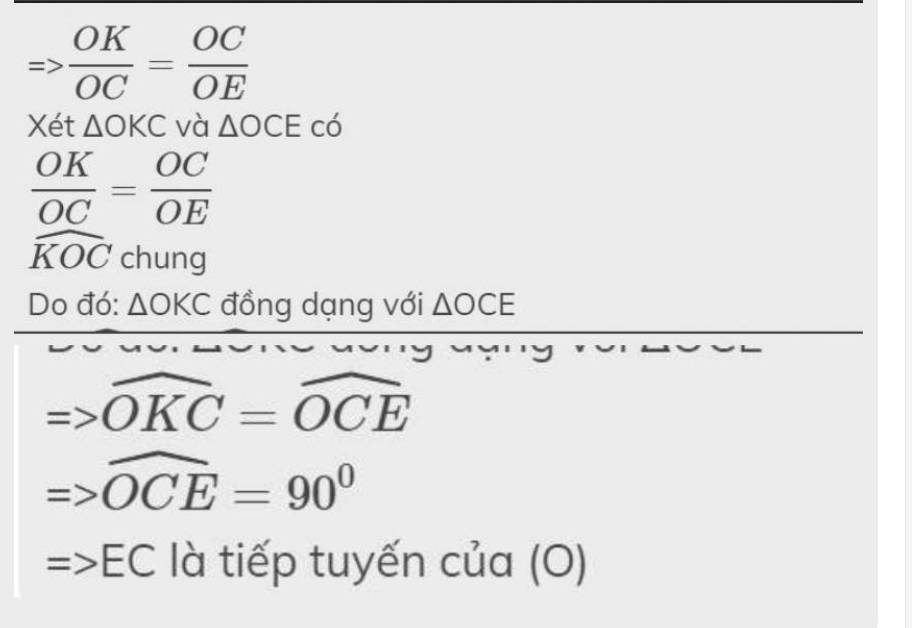
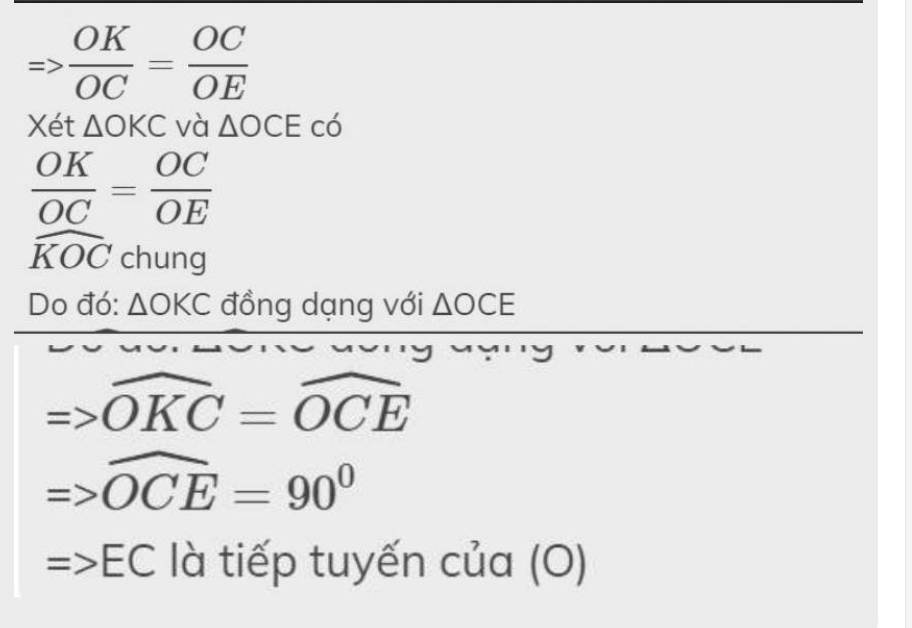
=>\(\dfrac{OI}{OC}=\dfrac{OC}{OK}\)
Xét ΔOIC và ΔOCK có
\(\dfrac{OI}{OC}=\dfrac{OC}{OK}\)
\(\widehat{IOC}\) chung
Do đó: ΔOIC đồng dạng với ΔOCK
=>\(\widehat{OIC}=\widehat{OCK}\)
=>\(\widehat{OCK}=90^0\)
=>KC là tiếp tuyến của (O)


b: Xét (O) có
ΔCAB nội tiếp
CB là đường kính
Do đó: ΔCAB vuông tại A
=>CA\(\perp\)AB tại A
=>CA\(\perp\)BE tại A
Ta có: \(\widehat{OAE}=\widehat{OAC}+\widehat{EAC}=\widehat{OAC}+90^0\)
\(\widehat{MAC}=\widehat{MAO}+\widehat{OAC}=\widehat{OAC}+90^0\)
Do đó: \(\widehat{OAE}=\widehat{MAC}\)
Xét tứ giác CKAE có \(\widehat{CKE}=\widehat{CAE}=90^0\)
nên CKAE là tứ giác nội tiếp
=>\(\widehat{ACK}=\widehat{AEK}\)
=>\(\widehat{ACM}=\widehat{AEO}\)
Xét ΔAMC và ΔAOE có
\(\widehat{ACM}=\widehat{AEO}\)
\(\widehat{MAC}=\widehat{OAE}\)
Do đó: ΔAMC đồng dạng với ΔAOE
=>\(\dfrac{AM}{AO}=\dfrac{AC}{AE}\)
=>\(AM\cdot AE=AO\cdot AC\)













a: Xét (O) có
MA,MB là tiếp tuyến
nên MA=MB
mà OA=OB
nên OM là trung trực của AB
Xét ΔOAM vuông tại A có AI là đường cao
nên OI*OM=OA^2=R^2
b: Xét ΔOIF vuông tại I và ΔOEM vuông tại E có
góc IÒ chung
Do đó: ΔOIF đồng dạng với ΔOEM
=>OI/OE=OF/OM
=>OE*OF=OI*OM=OA^2=OC^2=R^2
=>FC là tiếp tuyến của (O)