Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

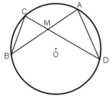
TH1: M nằm trong đường tròn.
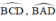 là hai góc nội tiếp cùng chắn cung
là hai góc nội tiếp cùng chắn cung 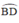
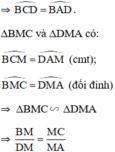
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
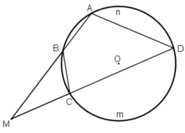
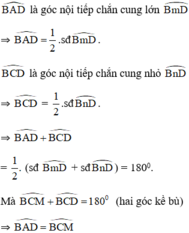
ΔMBC và ΔMDA có:
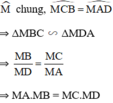
Kiến thức áp dụng
+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.
+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.

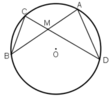
TH1: M nằm trong đường tròn.
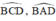 là hai góc nội tiếp cùng chắn cung
là hai góc nội tiếp cùng chắn cung 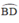
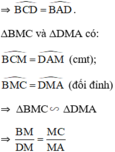
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
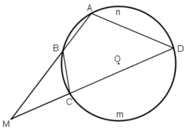
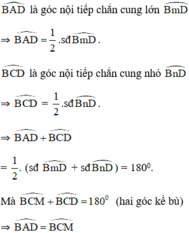
ΔMBC và ΔMDA có:
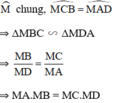

Xét (O) có
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ADC}=\widehat{ABC}\)
=>\(\widehat{MDA}=\widehat{MBC}\)
Xét ΔMDA và ΔMBC có
\(\widehat{MDA}=\widehat{MBC}\)
\(\widehat{M}\) chung
Do đó: ΔMDA đồng dạng với ΔMBC
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MC}\)
=>\(MD\cdot MC=MB\cdot MA\)

a) M ở bên trong đường tròn (hình a)

Xét hai tam giác MAB' và MA'B chúng có:
=
( đối đỉnh)
=
(hai góc nội tiếp cùng chắn cung
![]() ).
).
Do đó ∆MAB' ~ ∆MA'B, suy ra:
=
, do đó MA. MB = MB'. MA'
b) M ở bên ngoài đường tròn (hình b)

∆MAB' ~ ∆MA'B
M chung =
(hai góc nội tiếp cùng chắn cung
![]() ).
).
Suy ra: =
hay MA. MB = MB'. MA'

a ) Ta có : PA // BC => ^MPE = ^ECB = ^PBM vì PB là tiếp tuyến của (O)
=> \(\Delta MPE~\Delta MBP\left(g.g\right)\)
\(\Rightarrow\frac{MP}{MB}=\frac{ME}{MP}\Rightarrow MP^2=ME.MB\)
b ) .Ta có MA là tiếp tuyến của (O)
\(\Rightarrow\widehat{MAE}=\widehat{MBA}\Rightarrow\Delta MAE~\Delta MBA\left(g.g\right)\)
\(\Rightarrow\frac{MA}{MB}=\frac{ME}{MA}\Rightarrow MA^2=ME.MB\)
\(\Rightarrow MA^2=MP^2\Rightarrow MA=MP\Rightarrow M\) là trung điểm PA
Xét `2 triangle MBC` và `triangle MDA`.
`hatM` chung
`hat(ABC) = hat(MDA)` vì cùng chắn cung `AC`.
`=> triangle MBC = triangle MDA (g-g)`.
`-> (MB)/(MC) = (MD)/(MA).`
`=> MA . MB = MC . MD`.